Sun, Jan 4, 2026 https://atcoder.jp/contests/abc439
A. 2^n - 2*n https://atcoder.jp/contests/abc439/tasks/abc439_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
cout << (1ll << N) - (N * 2 ) << endl;
}
B. Happy Number https://atcoder.jp/contests/abc439/tasks/abc439_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
set< ll> memo;
while (N != 1 ) {
ll sum = 0 ;
while (N) {
ll m = N % 10 ;
sum += m * m;
N /= 10 ;
}
if (memo.count(sum)) {
No();
return ;
}
memo.insert(sum);
N = sum;
}
Yes();
}
C. 2026 https://atcoder.jp/contests/abc439/tasks/abc439_c
Wed, Dec 31, 2025 https://atcoder.jp/contests/abc428
https://atcoder.jp/contests/abc428/tasks/abc428_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll S, A, B, X;
cin >> S >> A >> B >> X;
ll ans = 0 ;
ans += S * A * (X / (A + B));
ans += S * min(A, X % (A + B));
cout << ans << endl;
}
B. Most Frequent Substrings https://atcoder.jp/contests/abc428/tasks/abc428_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, K;
string S;
cin >> N >> K >> S;
map< string, ll> cnt;
rep(i, N - K + 1 ) {
cnt[S.substr(i, K)]++ ;
}
ll mx = 0 ;
for (auto [k, v] : cnt) chmax(mx, v);
vector< string> ans;
for (auto [k, v] : cnt)
if (v == mx) ans.push_back(k);
sort(all(ans));
cout << mx << endl;
print(ans);
}
C. Brackets Stack Query https://atcoder.jp/contests/abc428/tasks/abc428_c
Mon, Dec 29, 2025 https://atcoder.jp/contests/abc431
A. Robot Balance https://atcoder.jp/contests/abc431/tasks/abc431_a
B. Robot Weight https://atcoder.jp/contests/abc431/tasks/abc431_b
C. Robot Factory https://atcoder.jp/contests/abc431/tasks/abc431_c
D. Robot Customize https://atcoder.jp/contests/abc431/tasks/abc431_d
すべてのパーツを体につけることはできるので嬉しさは $\sum_i B_i$ 以上であることが言える。
すべてのパーツを体につけたあとにいくつかを頭に付け替えることで嬉しさを最大化させたい。
例えば $i$ 番目のパーツを頭に付け替えると、嬉しさは $H_i - B_i$ 変化する。
$V_i = H_i - B_i$ とし、重さの和が $w$ のときの $V_i$ の和の最大値を dp を使って求める。
$w \leq \frac{\sum_i W_i}{2}$ を満たす$w$ について、$dp[w] + \sum_i B_i$ の最大値が答えとなる。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll W(N), H(N), B(N);
rep(i, N) cin >> W[i] >> H[i] >> B[i];
ll sumb = accumulate(all(B), 0ll );
ll sumw = accumulate(all(W), 0ll );
vll dp(500 * 500 + 5 , - INF);
dp[0 ] = 0 ;
rep(k, N) {
ll w = W[k], h = H[k], b = B[k];
for (ll i = 500 * 500 ; i > 0 ; i-- ) {
if (i - w < 0 ) continue ;
if (dp[i - w] == - INF) continue ;
chmax(dp[i], dp[i - w] + h - b);
}
}
ll ans = sumb;
rep(w, sumw / 2 + 1 ) {
chmax(ans, dp[w] + sumb);
}
cout << ans << endl;
}
$H_i \leq B_i$ であればそのパーツは頭につけるメリットはないので体につけるとしてよいので DP をするときもそれらのパーツは考慮しなくても良いけど、入れても問題ない。
Tue, Dec 23, 2025 https://atcoder.jp/contests/abc435
A. Triangular Number https://atcoder.jp/contests/abc435/tasks/abc435_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
cout << N * (N + 1 ) / 2 << endl;
}
B. No-Divisible Range https://atcoder.jp/contests/abc435/tasks/abc435_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll A(N);
rep(i, N) cin >> A[i];
fenwick_tree< ll> fw(N);
rep(i, N) fw.add(i, A[i]);
ll ans = 0 ;
rep(i, N) rep2(j, i, N) {
ll sum = fw.sum(i, j + 1 );
int div = 0 ;
rep2(k, i, j + 1 ) {
if (sum % A[k] == 0 ) div = 1 ;
}
if (! div) ans++ ;
}
cout << ans << endl;
}
C. Domino https://atcoder.jp/contests/abc435/tasks/abc435_c
Sun, Dec 21, 2025 https://atcoder.jp/contests/abc437
A. Feet https://atcoder.jp/contests/abc437/tasks/abc437_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll A, B;
cin >> A >> B;
cout << A * 12 + B << endl;
}
B. Tombola https://atcoder.jp/contests/abc437/tasks/abc437_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll H, W, N;
cin >> H >> W >> N;
vvll grid(H, vll(W));
rep(i, H) rep(j, W) {
cin >> grid[i][j];
}
ll ans = 0 ;
set< ll> B;
rep(i, N) {
ll x;
cin >> x;
B.insert(x);
}
rep(_, N) {
rep(i, H) {
ll tmp = 0 ;
rep(j, W) {
if (B.count(grid[i][j])) tmp++ ;
}
chmax(ans, tmp);
}
}
cout << ans << endl;
}
C. Reindeer and Sleigh 2 https://atcoder.jp/contests/abc437/tasks/abc437_c
Sun, Oct 5, 2025 https://atcoder.jp/contests/abc426
A. OS Versions https://atcoder.jp/contests/abc426/tasks/abc426_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string X, Y;
cin >> X >> Y;
map< string, int > mp;
mp["Ocelot" ] = 1 ;
mp["Serval" ] = 2 ;
mp["Lynx" ] = 3 ;
yesno(mp[X] >= mp[Y]);
}
B. The Odd One Out https://atcoder.jp/contests/abc426/tasks/abc426_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string S;
cin >> S;
map< char , int > mp;
for (char c : S) mp[c]++ ;
for (auto [k, v] : mp) {
if (v == 1 ) {
cout << k << endl;
}
}
}
C. Upgrade Required https://atcoder.jp/contests/abc426/tasks/abc426_c
Sun, Sep 28, 2025 https://atcoder.jp/contests/abc425
A. Sigma Cubes https://atcoder.jp/contests/abc425/tasks/abc425_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
ll ans = 0 ;
rep2(i, 1 , N + 1 ) {
ans += intpow(- 1 , i) * intpow(i, 3 );
}
cout << ans << endl;
}
B. Find Permutation 2 https://atcoder.jp/contests/abc425/tasks/abc425_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll A(N);
rep(i, N) cin >> A[i];
vint P(N);
iota(all(P), 1 );
do {
int ok = 1 ;
rep(i, N) {
if (A[i] == - 1 ) continue ;
if (A[i] != P[i]) ok = 0 ;
}
if (ok) {
Yes();
print(P);
return ;
}
} while (next_permutation(all(P)));
No();
}
C. Rotate and Sum Query https://atcoder.jp/contests/abc425/tasks/abc425_c
Mon, Sep 22, 2025 https://atcoder.jp/contests/abc424
A. Isosceles https://atcoder.jp/contests/abc424/tasks/abc424_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
vint v(3 );
rep(i, 3 ) cin >> v[i];
sort(all(v));
yesno(v[0 ] == v[1 ] || v[1 ] == v[2 ]);
}
B. Perfect https://atcoder.jp/contests/abc424/tasks/abc424_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, M, K;
cin >> N >> M >> K;
vint A(K), B(K);
rep(i, K) {
cin >> A[i] >> B[i];
A[i]-- , B[i]-- ;
}
vvint sol(N, vint(M));
vint ans;
rep(i, K) {
sol[A[i]][B[i]] = 1 ;
int cnt = 0 ;
rep(j, M) if (sol[A[i]][j]) cnt++ ;
if (cnt == M) ans.push_back(A[i] + 1 );
}
print(ans);
}
C. New Skill Acquired https://atcoder.jp/contests/abc424/tasks/abc424_c
Fri, Sep 19, 2025 https://atcoder.jp/contests/abcjoi2012yo
A. ランチ (Lunch) https://atcoder.jp/contests/joi2012yo/tasks/joi2012yo_a
B. サッカー (Soccer) https://atcoder.jp/contests/joi2012yo/tasks/joi2012yo_b
C. 最高のピザ (Best Pizza) https://atcoder.jp/contests/joi2012yo/tasks/joi2012yo_c
D. パスタ (Pasta) https://atcoder.jp/contests/joi2012yo/tasks/joi2012yo_d
E. イルミネーション (Illumination) https://atcoder.jp/contests/joi2012yo/tasks/joi2012yo_e
F. ジグザグ数 (Zig-Zag Numbers) https://atcoder.jp/contests/joi2012yo/tasks/joi2012yo_f
桁 DP 解法だということをわかった状態で自力 AC.
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
modint:: set_mod(10000 );
using mint = modint;
auto f = [& ](string X, ll MOD) -> mint {
int N = X.size();
// dp[is_less][prev number][dir][mod]
// dir: 0 不定, 1 up, 2 down
2 , vector(10 , vector(3 , vector< mint> (MOD))));
dp[0 ][0 ][0 ][0 ] = 1 ;
rep(i, N) {
int t = X[i] - '0' ;
vector dpn(2 , vector(10 , vector(3 , vector< mint> (MOD))));
rep(d, 10 ) rep(is_less, 2 ) rep(prev_number, 10 ) rep(dir, 3 ) rep(mod, MOD) {
if (! is_less && d > t) continue ;
if (dir == 1 && prev_number <= d) continue ;
if (dir == 2 && prev_number >= d) continue ;
if (dir == 0 && d != 0 && prev_number == d) continue ;
int is_less_n = is_less || d < t;
int dir_n = 0 ;
if (dir == 0 && prev_number == 0 ) {
dir_n = 0 ;
} else if (prev_number < d) {
dir_n = 1 ;
} else if (prev_number > d) {
dir_n = 2 ;
}
int mod_n = (mod * 10 + d) % MOD;
dpn[is_less_n][d][dir_n][mod_n] += dp[is_less][prev_number][dir][mod];
}
swap(dp, dpn);
}
mint ans = 0 ;
rep(is_less, 2 ) rep(d, 10 ) rep(dir, 3 ) {
ans += dp[is_less][d][dir][0 ];
}
// cout << ans << endl;
return ans;
};
string A, B;
ll M;
cin >> A >> B >> M;
ll zigzag = 0 ;
{
ll m = (A[0 ] - '0' ) % M;
rep2(i, 1 , (ll)A.size()) {
m *= 10 ;
m += A[i] - '0' ;
m %= M;
}
int ok = 1 ;
rep(i, (ll)A.size() - 1 ) {
if (A[i] == A[i + 1 ]) {
ok = 0 ;
break ;
}
}
rep2(i, 1 , (ll)A.size() - 1 ) {
if (A[i - 1 ] < A[i] && A[i] < A[i + 1 ]) ok = 0 ;
if (A[i - 1 ] > A[i] && A[i] > A[i + 1 ]) ok = 0 ;
}
zigzag = m == 0 && ok;
}
mint ans = f(B, M) - f(A, M) + zigzag;
cout << ans.val() << endl;
}
Thu, Sep 18, 2025 https://atcoder.jp/contests/abc129
A. Airplane https://atcoder.jp/contests/abc129/tasks/abc129_a
B. Balance https://atcoder.jp/contests/abc129/tasks/abc129_b
C. Typical Stairs https://atcoder.jp/contests/abc129/tasks/abc129_c
D. Lamp https://atcoder.jp/contests/abc129/tasks/abc129_d
E. Sum Equals Xor https://atcoder.jp/contests/abc129/tasks/abc129_e
桁 DP の問題ということをわかった状態で自力 AC.
$a+b = a XOR b$ の条件から $a$ と $b$ の各桁において同時に 1 にならないことがわかる.
$i$ 桁目が 0 のとき, $a_i, b_i$ は (0,0) のみ、$i$ 桁目が 1 のとき, $a_i, b_i$ は (0,1), (1,0) の 2 通りある。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string L;
cin >> L;
// dp[is_less]
< mint> dp(2 );
dp[0 ] = 1 ;
int N = L.size();
rep(i, N) {
int t = L[i] - '0' ;
vector< mint> dpn(2 );
rep(d, 2 ) rep(is_less, 2 ) {
if (! is_less && d > t) continue ;
int is_less_n = is_less || d < t;
ll mul = d == 0 ? 1 : 2 ;
dpn[is_less_n] += dp[is_less] * mul;
}
swap(dp, dpn);
}
cout << (dp[0 ] + dp[1 ]).val() << endl;
}
F. Takahashi’s Basics in Education and Learning https://atcoder.jp/contests/abc129/tasks/abc129_f
Mon, Sep 15, 2025 https://atcoder.jp/contests/code-festival-2014-quala
D - 壊れた電卓 桁 DP の問題とわかった状態でものすごい時間をかけて自力で AC したが、嘘解放だった。
rate 高い人のコードを参考にしたがそれでも嘘解放が結構多かったので難しい問題と思われる。
A 以下の数のうち条件を満たす最大値と、A 以上の数のうち条件を満たす最小値を求めて、その差の最小値を求める問題。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll A, K;
cin >> A >> K;
string S = to_string(A);
// dp[comp][used]
// comp = 0: A と同じ
// comp = 1: A より小さい
// comp = 2: A より大きい
// used: 使用した数の集合
3 , vll(1 << 10 , - 1 ));
dp[0 ][0 ] = 0 ;
rep(j, 1 << 10 ) dp[2 ][j] = INF;
int N = S.size();
rep(i, N) {
int t = S[i] - '0' ;
vector dpn(3 , vll(1 << 10 , - 1 ));
rep(j, 1 << 10 ) dpn[2 ][j] = INF;
rep(d, 10 ) rep(comp, 3 ) rep(used, 1 << 10 ) {
if (dp[comp][used] < 0 ) continue ;
if (dp[comp][used] == INF) continue ;
int comp_n = comp;
if (comp == 0 ) {
if (d < t) comp_n = 1 ;
if (d > t) comp_n = 2 ;
}
int used_n = used | (1 << d);
if (used == 0 && d == 0 ) used_n = 0 ; // 0 が続いている場合は 0 を使っていないとみなす
if (comp_n <= 1 ) {
chmax(dpn[comp_n][used_n], dp[comp][used] * 10 + d);
} else {
chmin(dpn[comp_n][used_n], dp[comp][used] * 10 + d);
}
}
swap(dp, dpn);
}
ll ans = INF;
{
ll mx = 0 ;
ll mi = INF;
rep(used, 1 << 10 ) {
if (__builtin_popcountll(used) > K) continue ;
chmax(mx, max(dp[0 ][used], dp[1 ][used]));
chmin(mi, dp[2 ][used]);
}
chmin(ans, A - mx);
chmin(ans, mi - A);
}
cout << ans << endl;
}
AC されているコードでも嘘解放が比較的多い
Sun, Sep 14, 2025 https://atcoder.jp/contests/abc423
A. Scary Fee https://atcoder.jp/contests/abc423/tasks/abc423_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll X, C;
cin >> X >> C;
ll ans = X / (1000 + C) * 1000 ;
cout << ans << endl;
}
B. Locked Rooms https://atcoder.jp/contests/abc423/tasks/abc423_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vint keys(N);
rep(i, N) cin >> keys[i];
vll visited(N + 1 );
visited[0 ] = visited[N] = 1 ;
rep(i, N) {
if (keys[i] == 0 ) {
visited[i + 1 ] = 1 ;
} else {
break ;
}
}
for (int i = N - 1 ; i >= 0 ; i-- ) {
if (keys[i] == 0 )
visited[i] = 1 ;
else
break ;
}
ll cnt = 0 ;
rep(i, N + 1 ) if (! visited[i]) cnt++ ;
cout << cnt << endl;
}
C. Lock All Doors https://atcoder.jp/contests/abc423/tasks/abc423_c
Sun, Sep 7, 2025 https://atcoder.jp/contests/abc422
A. Stage Clear https://atcoder.jp/contests/abc422/tasks/abc422_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int i, j;
char c;
cin >> i >> c >> j;
if (j == 8 ) {
i++ ;
j = 1 ;
} else {
j++ ;
}
cout << i << '-' << j << endl;
}
B. Looped Rope https://atcoder.jp/contests/abc422/tasks/abc422_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int H, W;
cin >> H >> W;
vector< string> grid(H);
rep(i, H) cin >> grid[i];
vint di = {0 , 1 , 0 , - 1 };
vint dj = {1 , 0 , - 1 , 0 };
int ok = 1 ;
rep(i, H) rep(j, W) {
if (grid[i][j] == '.' ) continue ;
int cnt = 0 ;
rep(d, 4 ) {
int ni = i + di[d], nj = j + dj[d];
if (clamp(ni, 0 , H - 1 ) != ni || clamp(nj, 0 , W - 1 ) != nj) continue ;
if (grid[ni][nj] == '#' ) cnt++ ;
}
if (cnt == 2 || cnt == 4 ) continue ;
ok = 0 ;
}
yesno(ok);
}
C. AtCoder AAC Contest https://atcoder.jp/contests/abc422/tasks/abc422_c
Sun, Sep 7, 2025 https://atcoder.jp/contests/abc421
A. Misdelivery https://atcoder.jp/contests/abc421/tasks/abc421_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vector< string> S(N);
rep(i, N) cin >> S[i];
int X;
string Y;
cin >> X >> Y;
X-- ;
yesno(S[X] == Y);
}
B. Fibonacci Reversed https://atcoder.jp/contests/abc421/tasks/abc421_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll X, Y;
cin >> X >> Y;
auto f = [](ll x) -> ll {
string s = to_string(x);
reverse(all(s));
ll ret = stoll(s);
return ret;
};
vll A(11 );
A[1 ] = X, A[2 ] = Y;
rep2(i, 3 , 11 ) {
A[i] = f(A[i - 1 ] + A[i - 2 ]);
}
cout << A[10 ] << endl;
}
C. Alternated https://atcoder.jp/contests/abc421/tasks/abc421_c
Tue, Aug 26, 2025 https://atcoder.jp/contests/abc307
E. Distinct Adjacent https://atcoder.jp/contests/abc307/tasks/abc307_e
解説 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, M;
cin >> N >> M;
// dp[i][f]: i 番目の数が 0 番目の数と同じ(f=1)/違う(f=0)ときの場合の数
< mint> (2 ));
dp[0 ][1 ] = M;
rep2(i, 1 , N) {
// i 番目は 0 番目と同じ数字になる、かつ、同じ数字が連続してはいけないので i-1 番目の数は 0 番目の数とは違う
1 ] += dp[i - 1 ][0 ];
// i 番目が 0 番目と異なる数字のとき、i-1 番目の数は 0 番目と同じか異なるのどちらでもいける。
// i-1 番目の数が 0 番目と同じ時、i 番目の数は 0 番目とは違う M-1 通りが考えられる
// i-1 番目の数が 0 番目と異なる時、i 番目の数は 0 番目とは異なり i-1 番目の数とも異なるから M-2 通りが考えられる
0 ] += dp[i - 1 ][1 ] * (M - 1 ) + dp[i - 1 ][0 ] * (M - 2 );
}
cout << dp[N - 1 ][0 ].val() << endl;
}
Sun, Aug 24, 2025 https://atcoder.jp/contests/abc420
A. What month is it? https://atcoder.jp/contests/abc420/tasks/abc420_a
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll X, Y;
cin >> X >> Y;
X += Y;
X %= 12 ;
if (X == 0 ) X = 12 ;
cout << X << endl;
}
B. Most Minority https://atcoder.jp/contests/abc420/tasks/abc420_b
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, M;
cin >> N >> M;
vector< string> S(N);
rep(i, N) cin >> S[i];
vll scores(N);
rep(j, M) {
ll x = 0 , y = 0 ;
rep(i, N) {
if (S[i][j] == '0' )
x++ ;
else
y++ ;
}
if (x == 0 || y == 0 ) {
rep(i, N) scores[i]++ ;
continue ;
}
if (x < y) {
rep(i, N) {
if (S[i][j] == '0' ) scores[i]++ ;
}
} else {
rep(i, N) {
if (S[i][j] == '1' ) scores[i]++ ;
}
}
}
ll mx = 0 ;
rep(i, N) {
chmax(mx, scores[i]);
}
vll ans;
rep(i, N) if (scores[i] == mx) ans.push_back(i + 1 );
print(ans);
}
C. Sum of Min Query https://atcoder.jp/contests/abc420/tasks/abc420_c
Mon, Aug 11, 2025 https://atcoder.jp/contests/abc418
A. I’m a teapot https://atcoder.jp/contests/abc418/tasks/abc418_a
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
string S;
cin >> N >> S;
int m = S.size();
int ok = 1 ;
if (m < 3 ) {
ok = 0 ;
} else {
string subs = S.substr(m - 3 , 3 );
ok = subs == "tea" ;
}
yesno(ok);
}
B. You’re a teapot https://atcoder.jp/contests/abc418/tasks/abc418_b
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string S;
cin >> S;
double ans = 0.0 ;
int N = S.size();
rep(i, N) rep2(j, i + 1 , N) {
if (S[i] == 't' && S[j] == 't' && j - i >= 2 ) {
ll len = j - i + 1 ;
ll x = 0 ;
rep2(k, i, j + 1 ) if (S[k] == 't' ) x++ ;
chmax(ans, (double )(x - 2 ) / (double )(len - 2 ));
}
}
printf("%.15lf \n " , ans);
}
C. Flush https://atcoder.jp/contests/abc418/tasks/abc418_c
Mon, Aug 11, 2025 https://atcoder.jp/contests/abc417
A. A Substring https://atcoder.jp/contests/abc417/tasks/abc417_a
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, A, B;
cin >> N >> A >> B;
string S;
cin >> S;
for (int i = A; i < N - B; i++ ) cout << S[i];
cout << endl;
}
B. Search and Delete https://atcoder.jp/contests/abc417/tasks/abc417_b
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, M;
cin >> N >> M;
multiset< ll> A;
rep(i, N) {
ll a;
cin >> a;
A.insert(a);
}
rep(i, M) {
ll b;
cin >> b;
auto it = A.lower_bound(b);
if (* it == b) {
A.erase(it);
}
}
vll ans;
for (auto x : A) ans.push_back(x);
print(ans);
}
C. Distance Indicators https://atcoder.jp/contests/abc417/tasks/abc417_c
Fri, Aug 8, 2025 https://atcoder.jp/contests/arc123
A. Arithmetic Sequence https://atcoder.jp/contests/arc123/tasks/arc123_a
解説 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll a, b, c;
cin >> a >> b >> c;
ll x = b * 2 - a - c;
ll ans = 0 ;
if (x >= 0 ) {
ans = x;
} else {
x = abs(x);
ll q = (x + 1 ) / 2 ;
ll r = x % 2 ;
ans = q + r;
}
cout << ans << endl;
}
B. Increasing Triples https://atcoder.jp/contests/arc123/tasks/arc123_b
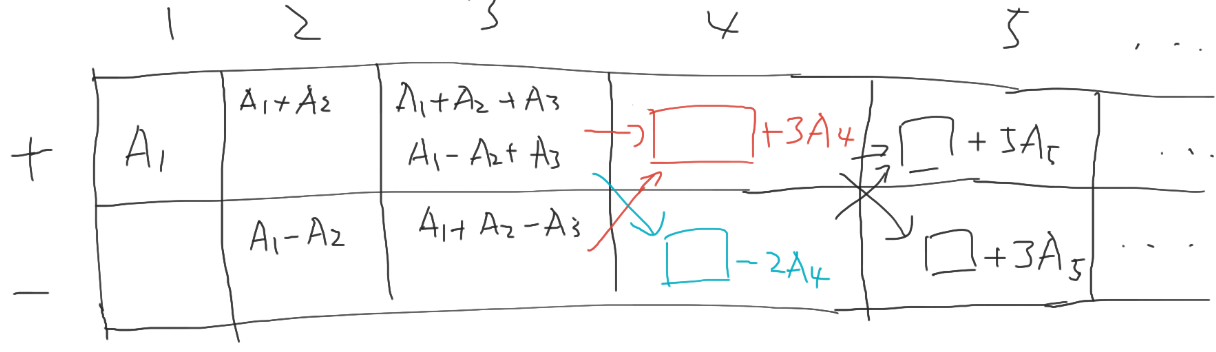
C. 1, 2, 3 - Decomposition https://atcoder.jp/contests/arc123/tasks/arc123_c
Thu, Aug 7, 2025 https://atcoder.jp/contests/arc124
A. LR Constraints https://atcoder.jp/contests/arc124/tasks/arc124_a
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, K;
cin >> N >> K;
vll v(N, K);
vll L, R;
rep(i, K) {
char c;
ll k;
cin >> c >> k;
k-- ;
if (c == 'L' ) {
L.push_back(k);
} else {
R.push_back(k);
}
}
sort(rall(L));
sort(rall(R));
for (ll k : L) {
rep(i, k) v[i]-- ;
}
for (ll k : R) {
rep2(i, k + 1 , N) v[i]-- ;
}
for (ll k : L) {
v[k] = 1 ;
}
for (ll k : R) {
v[k] = 1 ;
}
mint ans = 1 ;
rep(i, N) ans *= v[i];
cout << ans.val() << endl;
}
B. XOR Matching 2 https://atcoder.jp/contests/arc124/tasks/arc124_b
Fri, Aug 1, 2025 https://atcoder.jp/contests/arc151
A. Equal Hamming Distances https://atcoder.jp/contests/arc151/tasks/arc151_a
自力 AC.
文字列 $X, Y$ のハミング距離を $d(X, Y)$ とする。
はじめ $U = 0\cdots0$ で初期化し、位の小さい方から $i$ 桁目を変えたときに $|d(S, U) - d(T, U)|$ が小さくなるならそれを採用、そうでなければそのままにするということを繰り返す。
$|d(S, U) - d(T, U)|$ が 0 になったら終了。0 にならなかったら -1 を出力。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
string S, T;
cin >> S >> T;
string U = string(N, '0' );
reverse(all(S));
reverse(all(T));
ll sd = 0 , td = 0 ;
rep(i, N) {
sd += S[i] != U[i];
td += T[i] != U[i];
}
if (sd == td) {
cout << U << endl;
return ;
}
int ok = 0 ;
rep(i, N) {
ll tmps = sd, tmpt = td;
if (S[i] == '1' )
tmps-- ;
else
tmps++ ;
if (T[i] == '1' )
tmpt-- ;
else
tmpt++ ;
if (abs(tmps - tmpt) < abs(sd - td)) {
U[i] = '1' ;
sd = tmps;
td = tmpt;
}
if (sd == td) {
ok = 1 ;
break ;
}
}
reverse(all(U));
string ans = U;
if (! ok)
ans = "-1" ;
cout << ans << endl;
}
B. A < AP https://atcoder.jp/contests/arc151/tasks/arc151_b
Thu, Jul 31, 2025 https://atcoder.jp/contests/arc143
A. Three Integers https://atcoder.jp/contests/arc143/tasks/arc143_a
数日かけて自力 AC したが解説読んでもよくわからなかった。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll A, B, C;
cin >> A >> B >> C;
vll v = {A, B, C};
sort(all(v));
ll ans = 0 ;
if (v[0 ] < v[1 ]) {
ll d = v[1 ] - v[0 ];
ans += d;
v[1 ] -= d;
v[2 ] -= d;
}
if (v[1 ] < v[2 ]) {
ll d = v[2 ] - v[1 ];
ans += d * 2 ;
v[0 ] -= d;
v[1 ] -= d;
v[2 ] -= d * 2 ;
}
if (v[0 ] >= 0 && v[0 ] == v[1 ] && v[1 ] == v[2 ]) {
ans += v[0 ];
} else {
ans = - 1 ;
}
cout << ans << endl;
}
B. Counting Grids https://atcoder.jp/contests/arc143/tasks/arc143_b
Sun, Jul 27, 2025 https://atcoder.jp/contests/abc416
A. Vacation Validation https://atcoder.jp/contests/abc416/tasks/abc416_a
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, L, R;
cin >> N >> L >> R;
L-- , R-- ;
string S;
cin >> S;
int ok = 1 ;
for (int i = L; i <= R; i++ ) {
if (S[i] != 'o' ) ok = 0 ;
}
yesno(ok);
}
B. 1D Akari https://atcoder.jp/contests/abc416/tasks/abc416_b
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string S;
cin >> S;
int N = S.size();
string T;
T = S;
rep(i, N) if (T[i] != '#' ) {
T[i] = 'o' ;
}
rep(i, N) rep2(j, i + 1 , N) {
if (T[i] == 'o' && T[j] == 'o' ) {
int has = 0 ;
rep2(k, i + 1 , j) if (T[k] == '#' ) has = 1 ;
if (! has) T[j] = '.' ;
}
}
cout << T << endl;
}
C. Concat (X-th) https://atcoder.jp/contests/abc416/tasks/abc416_c
Tue, Jul 22, 2025 https://atcoder.jp/contests/abctdpc
A. コンテスト https://atcoder.jp/contests/tdpc/tasks/tdpc_contest
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll P(N);
rep(i, N) cin >> P[i];
int mx = (int )1e5 + 5 ;
vector< bool > dp(mx);
dp[0 ] = true;
rep(i, N) {
for (ll p = mx - 1 ; p >= 0 ; p-- ) {
if (p - P[i] >= 0 && dp[p - P[i]]) {
dp[p] = true;
}
}
}
ll ans = 0 ;
rep(i, mx) ans += dp[i];
cout << ans << endl;
}
B. ゲーム https://atcoder.jp/contests/tdpc/tasks/tdpc_game
Mon, Jul 21, 2025 https://atcoder.jp/contests/abc354
A. Exponential Plant https://atcoder.jp/contests/abc354/tasks/abc354_a
B. AtCoder Janken 2 https://atcoder.jp/contests/abc354/tasks/abc354_b
C. AtCoder Magics https://atcoder.jp/contests/abc354/tasks/abc354_c
D. AtCoder Wallpaper https://atcoder.jp/contests/abc354/tasks/abc354_d
E. Remove Pairs https://atcoder.jp/contests/abc354/tasks/abc354_e
自力 AC.
残りのカードの状態を $S_i$ とし、$S_i$ の状態からペアとなるカードの取り除き方が $m$ 通りあるとき、
$S_i$ からカードを除いた遷移先の状態を $S_{j_1}, \cdots, S_{j_m}$ とする。
$f(S_i)$ をカードの状態が $S_i$ で手番が来たときに勝てるか否かを表すとき
\begin{align*}
f(S_i) =
\begin{cases}
\text{true if } f(S_{j_k}) \text{のうち } f(S_{j_k}) = \text{false} \text{ がある} \\
\text{false otherwise}
\end{cases}
\end{align*}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll A(N), B(N);
rep(i, N) cin >> A[i] >> B[i];
vector< bool > fixed(1 << N), win(1 << N);
// 使われたカードの状態が state のときに手番が来たときに勝てるか
auto dfs = [& ](auto dfs, int state = 0 ) -> bool {
if (fixed[state]) return win[state];
vector< bool > ret;
// 表
+ 1 , N) {
if (! (state >> i & 1 ) && ! (state >> j & 1 ) && A[i] == A[j]) {
bool x = dfs(dfs, state | (1 << i) | (1 << j));
ret.push_back(x);
}
}
// 裏
+ 1 , N) {
if (! (state >> i & 1 ) && ! (state >> j & 1 ) && B[i] == B[j]) {
bool x = dfs(dfs, state | (1 << i) | (1 << j));
ret.push_back(x);
}
}
fixed[state] = true;
for (bool x : ret) {
if (! x) return win[state] = true;
}
return win[state] = false;
};
string ans = "Aoki" ;
if (dfs(dfs)) ans = "Takahashi" ;
cout << ans << endl;
}
F. Useless for LIS https://atcoder.jp/contests/abc354/tasks/abc354_f
Sun, Jul 20, 2025 https://atcoder.jp/contests/abc377
A. Rearranging ABC https://atcoder.jp/contests/abc377/tasks/abc377_a
B. Avoid Rook Attack https://atcoder.jp/contests/abc377/tasks/abc377_b
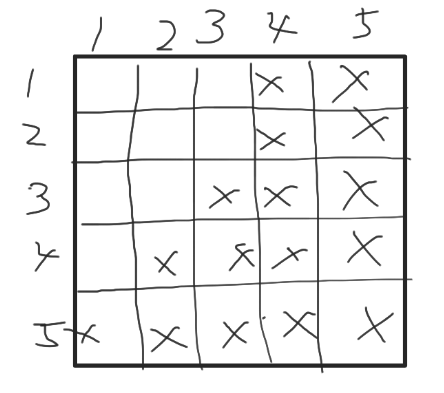
C. Avoid Knight Attack https://atcoder.jp/contests/abc377/tasks/abc377_c
D. Many Segments 2 https://atcoder.jp/contests/abc377/tasks/abc377_d
自力 AC.
考えられる区間 $\binom{M}{2} + M$ 個の中から、与えられた区間を完全に含むようなものの個数を引くことを考える。
まず、2つの区間 $[L_i, R_i], [L_j, R_j]$ に対して $L_i = L_j \wedge R_i < R_j$ となるようなものがあるとき、
$[L_j, R_j]$ を無視しても答えに影響はない。
よって $l = L_i$ となるような $i$ に対して $R_i$ の最小値だけを残すようにする。
左端を $l$ としたとき、区間の左端が $l$ 以降のものの中で右端が最小のものの座標を $r_{\min}$ とすると $M - r_{\min} + 1$ 個の区間は
何かしらの区間を完全に含むことになるのでその個数を引く。
これを $l = 1 \sim M$ に対して計算をする。
Sun, Jul 20, 2025 https://atcoder.jp/contests/arc160
A. Reverse and Count https://atcoder.jp/contests/arc160/tasks/arc160_a
B. Triple Pair https://atcoder.jp/contests/arc160/tasks/arc160_b
解説 AC.
解説の解説。
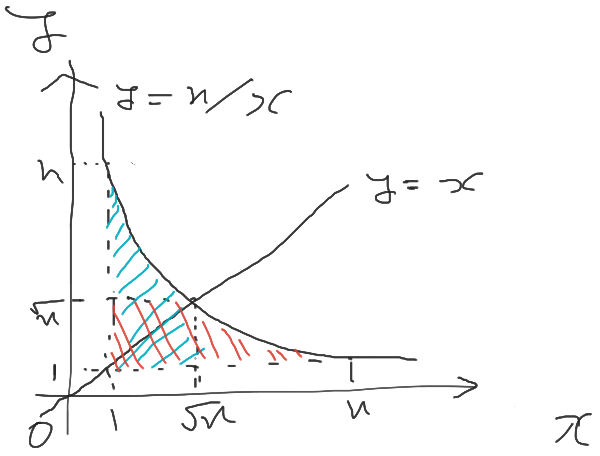
https://atcoder.jp/contests/arc160/editorial/6355 で出てくる $3 \times \sum_{i=M+1}^N \floor{N/i}^2$ の計算部分について($M = \floor{\sqrt{N}}$)。
愚直に for loop すると TLE する。この区間の中に $\floor{N/i}$ の種類は $O(\sqrt{N})$ 種類あるが、
$\floor{N/i} = \floor{N/j}, (i \neq j)$ となることがあるので同じ値を取るものがいくつあるかを数える必要がある。
整数 $t$ に対して $t = \floor{N/i} \in [1, \sqrt{N})$ となる $i$ の範囲について考える。
\begin{align*}
&t = \floor{N/i} \\
\Leftrightarrow &t \leq \frac{N}{i} < t + 1 \\
\Leftrightarrow &\frac{1}{t + 1} < i/N \leq \frac{1}{t} \\
\Leftrightarrow &\frac{N}{t + 1} < i \leq \frac{N}{t} \\
\Leftrightarrow &\floor{\frac{N}{t + 1}} + 1 \leq i \leq \floor{\frac{N}{t}}
\end{align*}
Sat, Jul 19, 2025 https://atcoder.jp/contests/abc415
A. Unsupported Type https://atcoder.jp/contests/abc415/tasks/abc415_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll A(N);
rep(i, N) cin >> A[i];
ll X;
cin >> X;
int ok = 0 ;
rep(i, N) if (A[i] == X) ok = 1 ;
yesno(ok);
}
B. Pick Two https://atcoder.jp/contests/abc415/tasks/abc415_b
void solve () {
ios base:: sync_with_stdio(false);
cin.tie(nullptr );
string S;
cin >> S;
vll ids;
rep(i, (ll)S.size()) {
if (S[i] == '#' ) ids.push_back(i + 1 );
}
for (ll i = 0 ; i < (ll)ids.size(); i += 2 ) {
cout << ids[i] << ',' << ids[i + 1 ] << endl;
}
}
C. Mixture https://atcoder.jp/contests/abc415/tasks/abc415_c
Fri, Jul 18, 2025 https://atcoder.jp/contests/arc004
A. 2点間距離の最大値 ( The longest distance ) https://atcoder.jp/contests/arc004/tasks/arc004_1
B. 2点間距離の最大と最小 ( Maximum and Minimum ) https://atcoder.jp/contests/arc004/tasks/arc004_2
C. 平均値太郎の憂鬱 ( The melancholy of Taro Heikinchi ) https://atcoder.jp/contests/arc004/tasks/arc004_3
解説 AC.
解説の補足
$X, Y$ を $\gcd(X,Y)$ で割って互いに素な整数とする。
\begin{align*}
&\frac{X}{Y} = \frac{\frac{1}{2}N(N+1) - M}{N} = \frac{N(N+1) - 2M}{2N} \\
\therefore ~~~ &2NX = \left\{ N(N+1) - 2M \right\} Y \\
\therefore ~~~ &2NX = \left\{ N(N+1) - 2M \right\} Y = kXY ~~~ (k \in \mathbb{Z}, \because \gcd(X,Y) = 1) \\
\therefore ~~~
&\left\{
\begin{aligned}
& 2N = kY \\
& N(N+1) - 2M = kX
\end{aligned} \\
\right.
\end{align*}
Wed, Jul 16, 2025 https://atcoder.jp/contests/abc300
A. N-choice question https://atcoder.jp/contests/abc300/tasks/abc300_a
B. Same Map in the RPG World https://atcoder.jp/contests/abc300/tasks/abc300_b
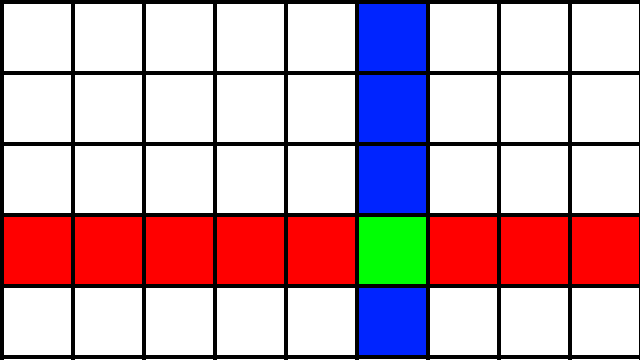
C. Cross https://atcoder.jp/contests/abc300/tasks/abc300_c
D. AABCC https://atcoder.jp/contests/abc300/tasks/abc300_d
$a < b < c$ と $300 \leq N \leq 10^{12}$ より素数は $10^6$ までのものを考えれば十分である。
$a^5 < a^2 b c^2 \leq N \Rightarrow a < N^{1/5} = ( 10^{12} )^{1/5} \approx 251.18$
$b^3 < b c^2 < N/a^2 \Rightarrow b < (N/a^2)^{1/3}$
\begin{align*}
\int_{1}^{(10^{ 12 })^{1/5}} \left( \frac{10^12}{x^2} \right)^{1/3} dx \approx 1.592 \times 10^5
\end{align*}
Wed, Jul 16, 2025 https://atcoder.jp/contests/abc166
A. A?C https://atcoder.jp/contests/abc166/tasks/abc166_a
B. Trick or Treat https://atcoder.jp/contests/abc166/tasks/abc166_b
C. Peaks https://atcoder.jp/contests/abc166/tasks/abc166_c
D. I hate Factorization https://atcoder.jp/contests/abc166/tasks/abc166_d
自力 AC したが、正当性が証明できなかったので嘘解法だったかもしれない。
$A^5 - B^5 = (A-B)(A^4 + A^3B + A^2B^2 + AB^3 + B^4)$ という因数分解できるので $A-B$ の値を $[1, \sqrt{X}]$ くらいの範囲で固定して
$A$ の値を $A^4 \leq X/(A-B)$ くらいの範囲で収まる $A$ で検索すればいいかなという感じで実装した。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll X;
cin >> X;
// A^5 - B^5 = (A-B)(A^4 + A^3*B + A^2*B^2 + A*B^3 + B^4)
for (ll d = 1 ; d * d <= X; d++ ) {
if (X % d != 0 ) continue ;
ll t = X / d;
for (ll a = 0 ; a * a * a * a <= t; a++ ) {
ll b = a - d;
if (a * a * a * a * a - b * b * b * b * b == X) {
cout << a << ' ' << b << endl;
return ;
}
}
}
}
正しい解法
Tue, Jul 15, 2025 https://atcoder.jp/contests/abcdiverta2019
A. Consecutive Integers https://atcoder.jp/contests/diverta2019/tasks/diverta2019_a
B. RGB Boxes https://atcoder.jp/contests/diverta2019/tasks/diverta2019_b
C. AB Substrings https://atcoder.jp/contests/diverta2019/tasks/diverta2019_c
D. DivRem Number https://atcoder.jp/contests/diverta2019/tasks/diverta2019_d
条件より $N = qm + r = rm + r = r(m+1), (0 \leq r < m)$ となる。
ここで合成数 $M = ab, avoid solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
ll ans = 0 ;
for (ll r = 1 ; r * r <= N; r++ ) {
if (N % r != 0 ) continue ;
ll m = N / r;
m-- ;
if (r < m) ans += m;
}
cout << ans << endl;
}
E. XOR Partitioning https://atcoder.jp/contests/diverta2019/tasks/diverta2019_e
Sun, Jul 13, 2025 https://atcoder.jp/contests/arc161
A. Make M https://atcoder.jp/contests/arc161/tasks/arc161_a
解説 AC.
方針はあっていたが実装ミスした。
rep(i, v.size()) {
v.pop_back();
}
v の中身を全部舐めるために上記のような書き方をしてしまったが、これだと i がインクリメントされるのに対して上限の v.size() が減っていくため
v 全体を舐められていなかった。
while (v.size()) のようにするか、予め size の値を保存にしてからループを回す必要があった。
$A$ をソートして前半半分を奇数番目の数字に、後半半分を偶数番目の数字にする。
順番はソートされたままの状態にする。
このときに、M型になるか判定すればよい。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll A(N);
rep(i, N) cin >> A[i];
sort(all(A));
vll f, b;
rep(i, ceil(N, 2 )) f.push_back(A[i]);
rep2(i, ceil(N, 2 ), N) b.push_back(A[i]);
int ok = 1 ;
while (b.size()) {
if (f.back() < b.back()) {
f.pop_back();
b.pop_back();
} else {
ok = 0 ;
break ;
}
}
yesno(ok);
}
B. Exactly Three Bits https://atcoder.jp/contests/arc161/tasks/arc161_b
Sat, Jul 12, 2025 https://atcoder.jp/contests/abc414
A. Streamer Takahashi https://atcoder.jp/contests/abc414/tasks/abc414_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, L, R;
cin >> N >> L >> R;
ll ans = 0 ;
rep(i, N) {
int x, y;
cin >> x >> y;
if (x <= L && R <= y) ans++ ;
}
cout << ans << endl;
}
B. String Too Long https://atcoder.jp/contests/abc414/tasks/abc414_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vector< pair< char , ll>> ps;
ll tot = 0 ;
rep(i, N) {
char c;
ll l;
cin >> c >> l;
ps.emplace_back(c, l);
tot += l;
if (tot > 100 ) {
cout << "Too Long" << endl;
return ;
}
}
for (auto [c, n] : ps) {
rep(i, n) cout << c;
}
cout << endl;
}
C. Palindromic in Both Bases https://atcoder.jp/contests/abc414/tasks/abc414_c
Fri, Jul 11, 2025 https://atcoder.jp/contests/arc165
A. Sum equals LCM https://atcoder.jp/contests/arc165/tasks/arc165_a
自力 AC.
(i) $N$ が素冪のとき
$N = p^x$ とかけるが $A_i$ のいずれかは $A_i = p^x$ とせねばならず $2 \leq n$ という制約では $A_1 + \cdots + A_n = N$ は成立しない。
(ii) $N$ が素冪でないとき
$N$ に含まれる素因数のうち異なる2つを $p$, $q$ ($p < q$) とする.
$A_1 = N/p$, $A_2 = N/q$ とすると
\begin{align*}
N - A_1 - A_2 &= N - \frac{N}{p} - \frac{N}{q} \\
&= N \left(1 - \frac{1}{p} - \frac{1}{q}\right) \\
&\geq N \left(1 - \frac{1}{p} - \frac{1}{p}\right) \\
&= N \left(1 - \frac{2}{p}\right) \\
&= N \left( \frac{p-2}{p} \right) \\
&\geq 0 ~~~(\because p \geq 2)
\end{align*}
Thu, Jul 10, 2025 https://atcoder.jp/contests/arc168
A. <Inversion> https://atcoder.jp/contests/arc168/tasks/arc168_a
自力 AC.
数字をうまいこと選ぶことによって下降する区間の転倒数について考えればよくできる。
具体的な構成方法としては公式解説 にある通りに作ればよい。
減少する区間の長さ $L$ のとき、転倒数は $L(L-1)/2$ であるから、$i$ 個目の減少する区間の長さが $L_i$ のとき、求める答えは $\sum_i L_i(L_i-1)/2$ となる。
区間の長さは文字列 $S$ をランレングス圧縮して > の個数+1 を使えばよい。
vector< pair< char , long long int >> runLengthEncode(const string& input) {
vector< pair< char , long long int >> encoded;
int size = input.size();
for (int i = 0 ; i < size; ++ i) {
long long int count = 1 ;
while (i + 1 < size && input[i] == input[i + 1 ]) {
++ i;
++ count;
}
encoded.emplace_back(input[i], count);
}
return encoded;
}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
string S;
cin >> N >> S;
auto ps = runLengthEncode(S);
ll ans = 0 ;
for (auto [c, x] : ps) {
if (c == '>' )
ans += (ll)x * (x + 1 ) / 2 ;
}
cout << ans << endl;
}
B. Arbitrary Nim https://atcoder.jp/contests/arc168/tasks/arc168_b
Thu, Jul 10, 2025 https://atcoder.jp/contests/arc171
A. No Attacking https://atcoder.jp/contests/arc171/tasks/arc171_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
auto cal = []() -> void {
ll N, A, B;
cin >> N >> A >> B;
bool ans = true;
if (A > N) ans = false;
// ポーンは奇数行目、ルークは偶数行目に置くのが最適
// ルークを偶数行目においてもまだ余っている場合は奇数行目におく
// 開いてる行数 * (N-A) が B 以上であれば良い配置にできる。そうでなければできない。
= (N + 1 ) / 2 * (N - A);
if (A > N / 2 ) {
mx -= (A - N / 2 ) * (N - A);
}
yesno(ans && B <= mx);
};
int t;
cin >> t;
rep(i, t) cal();
}
B. Chmax https://atcoder.jp/contests/arc171/tasks/arc171_b
Mon, Jul 7, 2025 https://atcoder.jp/contests/arc178
A. Good Permutation 2 https://atcoder.jp/contests/arc178/tasks/arc178_a
自力 AC.
$A$ の順序は問題に答えに影響しないので昇順にソートしておく。
$A$ の中に $1$ または $N$ が含まれている場合は、どのようにしても良い順列を作れないので -1 を出力する。
それ以外のときは $P_{A_i} = A_i + 1$ とし、確定していない部分は小さい順にまだ使用していない数字で埋めれば良い。
$A_1 = x$ のときで考えてみる。
辞書順で最小にしたいのでなるべく $1, 2, \cdots$ の順にしたいが $1, 2, \cdots, x$ とすると良い順列にならないので
最初の $x$ 個は $1, 2, \cdots, x-1, x+1$ とするのが最適である。
同様にして $P_{A_i} = A_i + 1$ としておけば良い順列の条件を満たす辞書順最小の順列が得られる。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, M;
cin >> N >> M;
vll A(M);
rep(i, M) cin >> A[i];
{
int ok = 1 ;
rep(i, M) {
if (A[i] == 1 || A[i] == N) ok = 0 ;
}
if (! ok) {
cout << - 1 << endl;
return ;
}
}
vll ans(N + 1 , - 1 );
vint used(N + 1 );
for (int a : A) {
ans[a] = a + 1 ;
used[a + 1 ] = 1 ;
}
queue< int > que;
rep2(i, 1 , N + 1 ) {
if (! used[i]) que.push(i);
}
rep2(i, 1 , N + 1 ) {
if (ans[i] < 0 ) {
ans[i] = que.front();
que.pop();
}
}
ans.erase(ans.begin(), ans.begin() + 1 );
print(ans);
}
B. 1 + 6 = 7 https://atcoder.jp/contests/arc178/tasks/arc178_b
Sun, Jul 6, 2025 https://atcoder.jp/contests/abc379
A. Cyclic https://atcoder.jp/contests/abc379/tasks/abc379_a
B. Strawberries https://atcoder.jp/contests/abc379/tasks/abc379_b
C. Sowing Stones https://atcoder.jp/contests/abc379/tasks/abc379_c
D. Home Garden https://atcoder.jp/contests/abc379/tasks/abc379_d
E. Sum of All Substrings https://atcoder.jp/contests/abc379/tasks/abc379_e
自力 AC.
サンプル 1 の 379 について考えてみる。
\begin{align*}
&3 + 37 + 379 + 7 + 79 + 9 \\
&= 3 + 7 + 7 + 9 + 9 + 9 + 30 + 70 + 70 + 300
\end{align*}
各位の寄与ごとに分解して考えてみる。
1 の位の寄与
Sat, Jul 5, 2025 https://atcoder.jp/contests/abc413
A. Content Too Large https://atcoder.jp/contests/abc413/tasks/abc413_a
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, M;
cin >> N >> M;
ll sum = 0 ;
rep(i, N) {
int a;
cin >> a;
sum += a;
}
yesno(sum <= M);
}
B. cat 2 https://atcoder.jp/contests/abc413/tasks/abc413_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vector< string> S(N);
rep(i, N) cin >> S[i];
set< string> memo;
rep(i, N) rep(j, N) {
if (i == j) continue ;
memo.insert(S[i] + S[j]);
}
cout << memo.size() << endl;
}
C. Large Queue https://atcoder.jp/contests/abc413/tasks/abc413_c
Sat, Jul 5, 2025 https://atcoder.jp/contests/arc180
A. ABA and BAB https://atcoder.jp/contests/arc180/tasks/arc180_a
自力 AC.
置換1: ABA -> A 置換2: BAB -> B とする。
ABABA… と A, B が交互に繰り返す文字列から文字を置換すると置換1, 2のどちらを使っても同じ文字列になり、また長さが2減る。
BABABA… と B, A が交互に繰り返す文字列についても同様。
文字が交互になる長さを $M$ とする. このとき置換によって生成される文字列のパターンは $\floor{(M+1)/2}$ 通りある。
文字が交互になる区間が $L$ 個あり、$i$ 個目の区間の長さが $m_i$ のとき答えは
\begin{align*}
\sum_{i=1}^{L} \floor{(m_i + 1) / 2} \mod 10^9 + 7
\end{align*}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
string S;
cin >> N >> S;
S.push_back(S.back());
mint ans = 1 ;
ll cnt = 1 ;
char p = S[0 ];
rep2(i, 1 , N + 1 ) {
if (p == S[i]) {
if (cnt >= 3 ) ans *= (cnt + 1 ) / 2 ;
cnt = 1 ;
} else {
cnt++ ;
}
p = S[i];
}
cout << ans.val() << endl;
}
B. Improve Inversions https://atcoder.jp/contests/arc180/tasks/arc180_b
Sat, Jul 5, 2025 https://atcoder.jp/contests/arc181
A. Sort Left and Right https://atcoder.jp/contests/arc181/tasks/arc181_a
自力 AC.
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
auto cal = []() -> void {
int N;
cin >> N;
vint P(N);
rep(i, N) {
cin >> P[i];
P[i]-- ;
}
vint v(N);
iota(all(v), 0 );
if (v == P) {
cout << 0 << endl;
return ;
}
int mx = - 1 ;
rep(i, N) {
if (i == P[i] && mx < P[i]) {
cout << 1 << endl;
return ;
}
chmax(mx, P[i]);
}
if (P.front() == N - 1 && P.back() == 0 )
cout << 3 << endl;
else
cout << 2 << endl;
};
int t;
cin >> t;
rep(i, t) cal();
}
B. Annoying String Problem https://atcoder.jp/contests/arc181/tasks/arc181_b
Sat, Jul 5, 2025 https://atcoder.jp/contests/arc183
https://atcoder.jp/contests/arc183/tasks/arc183_a
$N$ の偶奇によって場合分けする。
(i) $N$ が偶数のとき
長さ $NK$ の数列の順列のうち、前半半分は先頭の数字が $1, 2, \cdots, N/2$ から始まるものであり、後半半分は $N/2, \cdots, N$ から始まるものである。
求めるものは先頭の文字が $N/2$ のうち、辞書順で一番最後のものなので残りの数字を降順に並べて出力する
(ii) $N$ が奇数のとき
対称性より先頭の $K$ 個は $\floor{(N+1)/2}$ を $K$ 個並べる。
残りの数字を使って辞書順で真ん中になるものは $\floor{(N+1)/2}-1$ を一つ追加し、残りの数字を降順に並べる。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, K;
cin >> N >> K;
vint rem(N + 1 , K);
rem[0 ] = 0 ;
vint ans;
int x = (N + 1 ) / 2 ;
if (N % 2 == 0 ) {
ans.push_back(x);
rem[x]-- ;
} else {
rep(i, K) {
ans.push_back(x);
}
rem[x] = 0 ;
x-- ;
if (rem[x] > 0 ) {
ans.push_back(x);
rem[x]-- ;
}
}
for (int x = N; x >= 1 ; x-- ) {
rep(i, rem[x]) ans.push_back(x);
}
print(ans);
}
B. Near Assignment https://atcoder.jp/contests/arc183/tasks/arc183_b
Wed, Jul 2, 2025 https://atcoder.jp/contests/arc195
A. Twice Subsequence https://atcoder.jp/contests/arc195/tasks/arc195_a
$A$ の前方から抜き出した $B$ に一致する部分列と、$A$ の後方から抜き出した $B$ に一致する部分列が異なれば Yes, そうでなければ No.
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, M;
cin >> N >> M;
vll A(N), B(M);
rep(i, N) cin >> A[i];
rep(i, M) cin >> B[i];
vint lid;
int j = 0 ;
rep(i, N) {
if (A[i] == B[j]) {
lid.push_back(i);
j++ ;
}
if (j == M) break ;
}
vint rid;
j = M - 1 ;
for (int i = N - 1 ; i >= 0 ; i-- ) {
if (A[i] == B[j]) {
rid.push_back(i);
j-- ;
}
if (j < 0 ) break ;
}
reverse(all(rid));
yesno((ll)rid.size() == M && (ll)lid.size() == M && rid != lid);
}
https://atcoder.jp/contests/arc195/tasks/arc195_b
Wed, Jul 2, 2025 https://atcoder.jp/contests/arc175
A. Spoon Taking Problem https://atcoder.jp/contests/arc175/tasks/arc175_a
解説 AC.
解説読んで言わんとすることは理解できたが、時間おいてまた解けるかというと自信ない。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll P(N);
rep(i, N) {
cin >> P[i];
P[i]-- ;
}
string S;
cin >> S;
auto calL = [& ]() -> mint {
mint ret = 1 ;
vint used(N);
rep(i, N) {
int now = P[i];
int r = (P[i] + 1 ) % N;
if (! used[r] && S[now] == 'R' ) {
ret = 0 ;
}
if (used[r] && S[now] == '?' ) {
ret *= 2 ;
}
used[now] = 1 ;
}
return ret;
};
auto calR = [& ]() -> mint {
mint ret = 1 ;
vint used(N);
rep(i, N) {
int now = P[i];
int l = P[i], r = (P[i] + 1 ) % N;
if (! used[l] && S[now] == 'L' ) {
ret = 0 ;
}
if (used[l] && S[now] == '?' ) {
ret *= 2 ;
}
used[r] = 1 ;
}
return ret;
};
mint ans = calL() + calR();
cout << ans.val() << endl;
}
B. Parenthesis Arrangement https://atcoder.jp/contests/arc175/tasks/arc175_b
Tue, Jul 1, 2025 https://atcoder.jp/contests/arc174
A. A Multiply https://atcoder.jp/contests/arc174/tasks/arc174_a
類題: https://atcoder.jp/contests/past202212-open/tasks/past202212_g
自力 AC. PAST 013 を解いていたので解けた。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, C;
cin >> N >> C;
vll A(N);
rep(i, N) cin >> A[i];
vll cumsum(N + 1 );
rep(i, N) {
cumsum[i + 1 ] = cumsum[i] + A[i];
}
ll ans = cumsum[N];
{
// max(f(l,r)) = max(f(0,r) - f(0,l))
// = max(f(0,r) - min_l (f(0,l)))
= - INF;
ll mi = 0 ;
rep2(i, 1 , N + 1 ) {
chmin(mi, cumsum[i - 1 ]);
chmax(t, cumsum[i] - mi);
}
t *= (C - 1 );
t += cumsum[N];
chmax(ans, t);
}
{
// min(f(l,r)) = min(f(0,r) - f(0,l))
// = min(f(0,r) - max_l (f(0,l)))
= INF;
ll mx = - INF;
rep2(i, 1 , N + 1 ) {
chmax(mx, cumsum[i - 1 ]);
chmin(t, cumsum[i] - mx);
}
t *= (C - 1 );
t += cumsum[N];
chmax(ans, t);
}
cout << ans << endl;
}
B. Bought Review https://atcoder.jp/contests/arc174/tasks/arc174_b
Tue, Jul 1, 2025 https://atcoder.jp/contests/arc172
A. Chocolate https://atcoder.jp/contests/arc172/tasks/arc172_a
自力 AC.
解説と解き方が違うが多分問題ないと思う。
1辺が大きいピースから切り出していく。
下図のうち 1 の部分が切り出す部分とする。
切り出した後 2, 3, 4 の領域に分割する。
分割した領域のうち、短辺が一番大きいものを取り出して次に大きいチョコのピースを切り出す。
これを繰り返す。
┌─────────────────────┬─────────────────┐
│ │ │
│ │ │
│ │ │
│ │ │
│ │ │
│ 1 │ 2 │
│ │ │
│ │ │
│ │ │
│ │ │
├─────────────────────┼─────────────────┤
│ │ │
│ │ │
│ 3 │ 4 │
│ │ │
└─────────────────────┴─────────────────┘
2, 3 の境界と、3, 4 の境界は切ってもいい理由
全てのピースの大きさが2の冪なので大きいピース切り出していくと、境界をまたぐようなピースの置き方はできないので切っても問題ない。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll H, W, N;
cin >> H >> W >> N;
vll A(N);
rep(i, N) cin >> A[i];
sort(rall(A));
rep(i, N) {
A[i] = 1 << A[i];
}
using P = tuple< ll, ll, ll> ;
priority_queue< P> pq;
pq.push({min(H, W), H, W});
int ok = 1 ;
rep(i, N) {
if (pq.size() == 0 ) {
ok = 0 ;
break ;
}
auto [_, h, w] = pq.top();
pq.pop();
if (A[i] <= min(h, w)) {
ll dw = w - A[i], dh = h - A[i];
if (dw > 0 ) {
pq.push({min(A[i], dw), A[i], dw});
}
if (dh > 0 ) {
pq.push({min(dh, A[i]), dh, A[i]});
}
if (dw > 0 && dh > 0 ) {
pq.push({min(dh, dw), dh, dw});
}
} else {
ok = 0 ;
}
}
yesno(ok);
}
B. AtCoder Language https://atcoder.jp/contests/arc172/tasks/arc172_b
Sun, Jun 29, 2025 https://atcoder.jp/contests/abc361
A. Insert https://atcoder.jp/contests/abc361/tasks/abc361_a
B. Intersection of Cuboids https://atcoder.jp/contests/abc361/tasks/abc361_b
C. Make Them Narrow https://atcoder.jp/contests/abc361/tasks/abc361_c
D. Go Stone Puzzle https://atcoder.jp/contests/abc361/tasks/abc361_d
E. Tree and Hamilton Path 2 https://atcoder.jp/contests/abc361/tasks/abc361_e
解説 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vector< vector< pair< ll, ll>>> graph(N);
vll C;
rep(i, N - 1 ) {
int a, b, c;
cin >> a >> b >> c;
a-- , b-- ;
C.push_back(c);
graph[a].push_back({b, c});
graph[b].push_back({a, c});
}
vll dist(N);
auto dfs = [& ](auto dfs, int now, int p) -> void {
for (auto [nx, c] : graph[now]) {
if (nx == p) continue ;
dist[nx] = dist[now] + c;
dfs(dfs, nx, now);
}
};
dfs(dfs, 0 , - 1 );
int s = - 1 ;
ll d = - 1 ;
rep(i, N) {
if (d < dist[i]) {
d = dist[i];
s = i;
}
}
rep(i, N) dist[i] = 0 ;
dfs(dfs, s, - 1 );
d = - 1 ;
rep(i, N) {
if (d < dist[i]) {
d = dist[i];
}
}
ll ans = accumulate(all(C), 0ll );
ans *= 2 ;
ans -= d;
cout << ans << endl;
}
F. x = a^b https://atcoder.jp/contests/abc361/tasks/abc361_f
Sun, Jun 29, 2025 https://atcoder.jp/contests/abc412
A. Task Failed Successfully https://atcoder.jp/contests/abc412/tasks/abc412_a
B. Precondition https://atcoder.jp/contests/abc412/tasks/abc412_b
C. Giant Domino https://atcoder.jp/contests/abc412/tasks/abc412_c
できるだけ大きいドミノを選ぶのが最適。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
auto cal = []() -> void {
int N;
cin >> N;
vll S(N);
rep(i, N) cin >> S[i];
ll st = S[0 ], fin = S[N - 1 ];
S.erase(S.begin(), S.begin() + 1 );
S.pop_back();
sort(all(S));
S.push_back(INF);
ll ans = 2 ;
ll pr = st;
rep(i, (ll)S.size() - 1 ) {
if (S[i] <= pr) continue ;
if (fin <= pr * 2 ) break ;
if (S[i] <= pr * 2 && S[i + 1 ] > pr * 2 ) {
pr = S[i];
ans++ ;
}
}
if (fin > pr * 2 ) ans = - 1 ;
cout << ans << '\n' ;
};
int T;
cin >> T;
rep(i, T) {
cal();
}
}
upper_bound を使うバージョン
Sat, Jun 28, 2025 https://atcoder.jp/contests/abc327
A. ab https://atcoder.jp/contests/abc327/tasks/abc327_a
B. A^A https://atcoder.jp/contests/abc327/tasks/abc327_b
C. Number Place https://atcoder.jp/contests/abc327/tasks/abc327_c
D. Good Tuple Problem https://atcoder.jp/contests/abc327/tasks/abc327_d
E. Maximize Rating https://atcoder.jp/contests/abc327/tasks/abc327_e
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll P(N + 1 );
rep(i, N) cin >> P[i + 1 ];
double INF = 100000 ;
// dp[i][num]: i番目までの問題を選んで、num 個選んだときの \sum_{i=1}^k (0.9)^{k-i} Q[i] の最大値
+ 1 , vector< double > (N + 1 , - INF));
dp[0 ][0 ] = 0 ;
rep2(i, 1 , N + 1 ) {
rep(num, i + 1 ) {
chmax(dp[i][num], dp[i - 1 ][num]);
if (dp[i - 1 ][num] != - INF)
chmax(dp[i][num + 1 ], dp[i - 1 ][num] * 0.9 + P[i]);
}
}
vector< double > pow(N + 1 ), prd(N + 1 );
pow[0 ] = prd[0 ] = 1 ;
rep2(i, 1 , N + 1 ) {
pow[i] = pow[i - 1 ] * 0.9 ;
prd[i] += pow[i] + prd[i - 1 ];
}
double ans = - INF;
rep2(num, 1 , N + 1 ) {
chmax(ans, dp[N][num] / prd[num - 1 ] - 1200.0 / sqrt(num));
}
printf("%.9lf \n " , ans);
}
F. Apples https://atcoder.jp/contests/abc327/tasks/abc327_f
Fri, Jun 27, 2025 https://atcoder.jp/contests/abc200
A. Century https://atcoder.jp/contests/abc200/tasks/abc200_a
B. 200th ABC-200 https://atcoder.jp/contests/abc200/tasks/abc200_b
C. Ringo’s Favorite Numbers 2 https://atcoder.jp/contests/abc200/tasks/abc200_c
D. Happy Birthday! 2 https://atcoder.jp/contests/abc200/tasks/abc200_d
解説 AC.
鳩の巣原理で解くというのは全く思いつかなかった。
総和の余りが $R$ になるような個数を DP で調べて、2以上のやつがあれば復元するという方法で最初解こうとしたが WA がどうしても取れなかった。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll A(N);
rep(i, N) {
cin >> A[i];
A[i] %= 200 ;
}
map< int , vvint> mp;
int n = min(N, 8ll );
rep2(i, 1 , 1 << n) {
vint v;
ll sum = 0 ;
rep(j, n) if ((i >> j) & 1 ) {
v.push_back(j + 1 );
sum += A[j];
}
sum %= 200 ;
mp[sum].push_back(v);
}
for (auto [k, vv] : mp) {
if (vv.size() >= 2 ) {
Yes();
rep(i, 2 ) {
cout << vv[i].size() << ' ' ;
print(vv[i]);
}
return ;
}
}
No();
}
dp 版でも実装できた。解説や解説放送と違い、dp[x][r] を x 個使って総和の余りが r となる場合の数とした。
WA になっていた原因は愚直に dp[x][r] を計算すると int64 に収まらないので、2個以上になったら2に抑えてしまうようにすればよかった。
Fri, Jun 27, 2025 https://atcoder.jp/contests/past202212-open
G - 区間和 解説 AC.
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vll A(N);
rep(i, N) cin >> A[i];
vll cumsum(N + 1 ), mi(N + 1 );
rep(i, N) {
cumsum[i + 1 ] = cumsum[i] + A[i];
}
ll ans = - INF;
rep2(i, 1 , N + 1 ) {
chmax(ans, cumsum[i] - mi[i - 1 ]);
mi[i] = min(mi[i - 1 ], cumsum[i]);
}
cout << ans << endl;
}
Sun, Jun 22, 2025 https://atcoder.jp/contests/abc411
A. Required Length https://atcoder.jp/contests/abc411/tasks/abc411_a
取り込んだ文字列が $L$ 文字以上か判定するだけ
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string P;
int L;
cin >> P >> L;
yesno((int )P.size() >= L);
}
B. Distance Table https://atcoder.jp/contests/abc411/tasks/abc411_b
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vll D(N);
rep2(i, 1 , N) cin >> D[i];
rep(i, N) {
ll sum = 0 ;
vll ans;
rep2(j, i + 1 , N) {
sum += D[j];
ans.push_back(sum);
}
print(ans);
}
}
C. Black Intervals https://atcoder.jp/contests/abc411/tasks/abc411_c
Thu, Jun 19, 2025 A. AB Palindrome https://atcoder.jp/contests/arc145/tasks/arc145_a
自力 AC.
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
string S;
cin >> S;
if (S.size() == 2 ) {
yesno(S[0 ] == S[1 ]);
return ;
}
yesno(! (S.front() == 'A' && S.back() == 'B' ));
}
B. AB Game https://atcoder.jp/contests/arc145/tasks/arc145_b
自力 AC.
茶色 Diff らしいがだいぶ難しく感じた。
$N < A$ のとき、Alice は確定で負け。
$N \geq A$ のときを考える。
(i) $A \leq B$ のとき
ゲーム $x \in [1, A-1]$ では Alice は石を取り除けないので負け。
ゲーム $x \in [A, N]$ では Alice が石を取り除けるだけ除くと $x \mod A < B$ となるので Alice が勝てる。
よって Alice が勝てるゲームの個数は $N-(A-1)$
Tue, Jun 17, 2025 https://atcoder.jp/contests/abc174
A. Air Conditioner https://atcoder.jp/contests/abc174/tasks/abc174_a
B. Distance https://atcoder.jp/contests/abc174/tasks/abc174_b
C. Repsept https://atcoder.jp/contests/abc174/tasks/abc174_c
D. Alter Altar https://atcoder.jp/contests/abc174/tasks/abc174_d
E. Logs https://atcoder.jp/contests/abc174/tasks/abc174_e
自力 AC.
全ての丸太の長さを $x$ 以下のする場合に必要な切る回数を $f(x)$ とする。
$f(x) \leq K$ を満たす最小の $x$ が求める答え。
これは二分探索で求めることができる。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, K;
cin >> N >> K;
vll A(N);
rep(i, N) cin >> A[i];
auto f = [& ](ll x) -> ll {
ll ret = 0 ;
for (ll a : A) ret += (a + x - 1 ) / x - 1 ;
return ret;
};
ll ac = INF, wa = 0 ;
while (ac - wa > 1 ) {
ll wj = (ac + wa) / 2 ;
if (f(wj) <= K) {
ac = wj;
} else {
wa = wj;
}
}
cout << ac << endl;
}
F. Range Set Query https://atcoder.jp/contests/abc174/tasks/abc174_f
Mon, Jun 16, 2025 https://atcoder.jp/contests/abc270
A. 1-2-4 Test https://atcoder.jp/contests/abc270/tasks/abc270_a
B. Hammer https://atcoder.jp/contests/abc270/tasks/abc270_b
C. Simple path https://atcoder.jp/contests/abc270/tasks/abc270_c
D. Stones https://atcoder.jp/contests/abc270/tasks/abc270_d
E. Apple Baskets on Circle https://atcoder.jp/contests/abc270/tasks/abc270_e
自力 AC.
$f(x)$ を $x$ 周したときに食べるりんごの個数が $K$ 未満になるかを判定する関数とすると
$f(x) = \text{true}$ となる最大の $x$ が周回できる回数の最大値となる。
この $x$ の値は二分探索で求めることができる。
周回によってりんごの個数は $A_i \leftarrow A_i - \min(A_i, x)$ に変化し、あとは愚直にシミュレーションをすればよい。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, K;
cin >> N >> K;
vll A(N);
rep(i, N) cin >> A[i];
auto f = [& ](ll x) -> bool {
ll cnt = 0 ;
rep(i, N) {
cnt += min(A[i], x);
}
return cnt < K;
};
ll ac = 0 , wa = INF;
while (abs(ac - wa) > 1 ) {
ll wj = (ac + wa) / 2 ;
if (f(wj)) {
ac = wj;
} else {
wa = wj;
}
}
rep(i, N) {
ll x = A[i];
K -= min(x, ac);
A[i] -= min(x, ac);
}
int i = 0 ;
while (K) {
if (A[i] > 0 ) {
K-- ;
A[i]-- ;
}
i++ ;
}
print(A);
}
F. Transportation https://atcoder.jp/contests/abc270/tasks/abc270_f
Mon, Jun 16, 2025 https://atcoder.jp/contests/abc329
A. Spread https://atcoder.jp/contests/abc329/tasks/abc329_a
B. Next https://atcoder.jp/contests/abc329/tasks/abc329_b
C. Count xxx https://atcoder.jp/contests/abc329/tasks/abc329_c
D. Election Quick Report https://atcoder.jp/contests/abc329/tasks/abc329_d
E. Stamp https://atcoder.jp/contests/abc329/tasks/abc329_e
F. Colored Ball https://atcoder.jp/contests/abc329/tasks/abc329_f
サイズが小さい方の箱の中身を移すという比較的自然な考え方で解けた。なぜ水色 diff なのか疑問。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, Q;
cin >> N >> Q;
vint col(N);
rep(i, N) cin >> col[i];
vector< set< int >> balls(N);
rep(i, N) balls[i].insert(col[i]);
rep(i, Q) {
int a, b;
cin >> a >> b;
a-- , b-- ;
if (balls[a].size() < balls[b].size()) {
for (ll x : balls[a]) balls[b].insert(x);
balls[a].clear();
} else {
for (ll x : balls[b]) balls[a].insert(x);
balls[b].clear();
swap(balls[a], balls[b]);
}
cout << balls[b].size() << endl;
}
}
G. Delivery on Tree https://atcoder.jp/contests/abc329/tasks/abc329_g
Sun, Jun 15, 2025 https://atcoder.jp/contests/abc410
A. G1 https://atcoder.jp/contests/abc410/tasks/abc410_a
B. Reverse Proxy https://atcoder.jp/contests/abc410/tasks/abc410_b
C. Rotatable Array https://atcoder.jp/contests/abc410/tasks/abc410_c
D. XOR Shortest Walk https://atcoder.jp/contests/abc410/tasks/abc410_d
コンテスト中考えていたこと $W_i < 2^{10}$ であるから、各頂点に到達した際の値はせいぜい $2^{10} = 1024$ 通りの値しかない。
頂点 $1$ から始めて各頂点に到達した際の値が新規であれば次の頂点に進み、すでに到達した値であればその頂点で止めるような処理を DFS で行えば良さそう。
親の方向に帰るのは無意味だと思ったけど有向グラフで行きと帰りで重みが違うことがあるから親に帰ることもありえるということを WA を出して気づいた。
計算量的に行けるか不安ではあったが辺の数が少ないので行けるかなぁと思って出したら AC した。
解説によると頂点倍化という手法らしい。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, M;
cin >> N >> M;
using P = pair< ll, ll> ;
vector< vector< P>> graph(N);
rep(i, M) {
ll u, v, w;
cin >> u >> v >> w;
u-- , v-- ;
graph[u].emplace_back(v, w);
}
vector used(N, vint(1 << 10 , 0 ));
used[0 ][0 ] = true;
auto dfs = [& ](auto dfs, int now, ll xor_sum) -> void {
for (auto [nx, w] : graph[now]) {
ll nx_xor_sum = xor_sum ^ w;
if (used[nx][nx_xor_sum]) continue ;
used[nx][nx_xor_sum] = true;
dfs(dfs, nx, nx_xor_sum);
}
};
dfs(dfs, 0 , 0 );
ll ans = INF;
rep(i, 1 << 10 ) {
if (used[N - 1 ][i]) chmin(ans, i);
}
if (ans == INF) ans = - 1 ;
cout << ans << endl;
}
E. Battles in a Row https://atcoder.jp/contests/abc410/tasks/abc410_e
Fri, Jun 13, 2025 https://atcoder.jp/contests/abc257
A. A to Z String 2 https://atcoder.jp/contests/abc257/tasks/abc257_a
B. 1D Pawn https://atcoder.jp/contests/abc257/tasks/abc257_b
C. Robot Takahashi https://atcoder.jp/contests/abc257/tasks/abc257_c
D. Jumping Takahashi 2 https://atcoder.jp/contests/abc257/tasks/abc257_d
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vector< tuple< ll, ll, ll>> nodes;
rep(i, N) {
ll x, y, P;
cin >> x >> y >> P;
nodes.emplace_back(x, y, P);
}
auto f = [& ](ll x) -> bool {
rep(s, N) {
vector< bool > used(N);
used[s] = true;
queue< int > que;
que.push(s);
while (que.size()) {
int now = que.front();
que.pop();
rep(nx, N) {
if (nx == now) continue ;
if (used[nx]) continue ;
auto [xi, yi, pi] = nodes[now];
auto [xj, yj, pj] = nodes[nx];
if (pi * x >= abs(xi - xj) + abs(yi - yj)) {
used[nx] = true;
que.push(nx);
}
}
}
ll sum = accumulate(all(used), 0 );
if (sum == N) return true;
}
return false;
};
ll ac = 0 ;
rep(i, N) rep(j, N) {
auto [xi, yi, pi] = nodes[i];
auto [xj, yj, pj] = nodes[j];
chmax(ac, abs(xi - xj) + abs(yi - yj));
}
ll wa = - 1 ;
while (ac - wa > 1 ) {
ll wj = (ac + wa) / 2 ;
if (f(wj))
ac = wj;
else
wa = wj;
}
cout << ac << endl;
}
E. Addition and Multiplication 2 https://atcoder.jp/contests/abc257/tasks/abc257_e
Tue, Jun 10, 2025 https://atcoder.jp/contests/abc117
A. Entrance Examination https://atcoder.jp/contests/abc117/tasks/abc117_a
B. Polygon https://atcoder.jp/contests/abc117/tasks/abc117_b
C. Streamline https://atcoder.jp/contests/abc117/tasks/abc117_c
D. XXOR https://atcoder.jp/contests/abc117/tasks/abc117_d
桁 DP で解ける問題だということをわかった上で自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, K;
cin >> N >> K;
vll A(N);
rep(i, N) cin >> A[i];
vint Kbit;
vvint Abit(N);
int mx = 60 ;
{
ll t = K;
rep(i, mx) {
Kbit.push_back(t % 2 );
t /= 2 ;
}
reverse(all(Kbit));
rep(i, N) {
ll a = A[i];
rep(j, mx) {
Abit[i].push_back(a % 2 );
a /= 2 ;
}
reverse(all(Abit[i]));
}
}
vector dp(mx + 1 , vll(2 ));
rep2(i, 1 , mx + 1 ) {
int t = Kbit[i - 1 ];
ll cnt = 0 ;
rep(j, N) {
cnt += Abit[j][i - 1 ];
}
rep(d, 2 ) {
if (d < t) {
chmax(dp[i][1 ], dp[i - 1 ][0 ] * 2 + cnt);
}
if (d == t) {
if (d == 0 )
chmax(dp[i][0 ], dp[i - 1 ][0 ] * 2 + cnt);
else
chmax(dp[i][0 ], dp[i - 1 ][0 ] * 2 + N - cnt);
}
if (dp[i - 1 ][1 ]) {
chmax(dp[i][1 ], dp[i - 1 ][1 ] * 2 + max(N - cnt, cnt));
}
}
}
cout << max(dp[mx][0 ], dp[mx][1 ]) << endl;
}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int m = 60 ;
auto f = [& ](ll x) -> vint {
vint v;
rep(i, m) {
v.push_back(x % 2 );
x /= 2 ;
}
reverse(all(v));
return v;
};
ll N, K;
cin >> N >> K;
vll A(N);
rep(i, N) cin >> A[i];
vint kbit = f(K);
vvint abits(N);
rep(i, N) {
abits[i] = f(A[i]);
}
// dp[is_less]
2 , - 1 );
dp[0 ] = 0 ;
rep(i, m) {
int t = kbit[i];
vll dpn(2 , - 1 );
rep(d, 2 ) rep(is_less, 2 ) {
if (! is_less && d > t) continue ; // K 超える数は NG
if (dp[is_less] == - 1 ) continue ; // 未到達な状態からの遷移は NG
int is_less_n = is_less || d < t;
ll cnt = 0 ;
for (vint& a : abits) {
cnt += a[i] ^ d;
}
chmax(dpn[is_less_n], dp[is_less] * 2 + cnt);
}
swap(dp, dpn);
}
cout << max(dp[0 ], dp[1 ]) << endl;
}
Mon, Jun 9, 2025 https://atcoder.jp/contests/abc007
A. 植木算 https://atcoder.jp/contests/abc007/tasks/abc007_1
B. 辞書式順序 https://atcoder.jp/contests/abc007/tasks/abc007_2
D. 禁止された数字 https://atcoder.jp/contests/abc007/tasks/abc007_4
桁 DP であるこということをわかった上で自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string A, B;
cin >> A >> B;
auto cal = [](string S) -> ll {
int N = S.size();
vector dp(N + 1 , vector(2 , vector(2 , vll(2 ))));
dp[0 ][0 ][0 ][0 ] = 1 ;
rep2(i, 1 , N + 1 ) {
int t = S[i - 1 ] - '0' ;
rep(d, 10 ) {
bool has_four = d == 4 ;
bool has_nine = d == 9 ;
if (d < t) {
rep(fr, 2 ) rep(ni, 2 ) {
dp[i][1 ][has_four || fr][has_nine || ni] += dp[i - 1 ][0 ][fr][ni];
}
}
if (t == d) {
rep(fr, 2 ) rep(ni, 2 ) {
dp[i][0 ][has_four || fr][has_nine || ni] += dp[i - 1 ][0 ][fr][ni];
}
}
rep(fr, 2 ) rep(ni, 2 ) {
dp[i][1 ][has_four || fr][has_nine || ni] += dp[i - 1 ][1 ][fr][ni];
}
}
}
ll ret = 0 ;
rep(fr, 2 ) rep(ni, 2 ) {
if (fr == 0 && ni == 0 ) continue ;
ret += dp[N][1 ][fr][ni] + dp[N][0 ][fr][ni];
}
return ret;
};
// cout << cal(B) << endl;
// cout << cal(A) << endl;
cout << cal(B) - cal(to_string(stoll(A) - 1 )) << endl;
}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
auto f = [](ll X) -> ll {
string S = to_string(X);
int N = S.size();
// dp[is_less][used_banned_number]
2 , vll(2 ));
dp[0 ][0 ] = 1 ;
rep(i, N) {
int t = S[i] - '0' ;
vector dpn(2 , vll(2 ));
rep(d, 10 ) rep(is_less, 2 ) rep(used, 2 ) {
if (! is_less && d > t) continue ;
int is_less_n = is_less || d < t;
int used_n = used || d == 4 || d == 9 ;
dpn[is_less_n][used_n] += dp[is_less][used];
}
swap(dp, dpn);
}
return dp[0 ][1 ] + dp[1 ][1 ];
};
ll A, B;
cin >> A >> B;
cout << f(B) - f(A - 1 ) << endl;
}
Mon, Jun 9, 2025 https://atcoder.jp/contests/abc154
A. Remaining Balls https://atcoder.jp/contests/abc154/tasks/abc154_a
B. I miss you https://atcoder.jp/contests/abc154/tasks/abc154_b
C. Distinct or Not https://atcoder.jp/contests/abc154/tasks/abc154_c
D. Dice in Line https://atcoder.jp/contests/abc154/tasks/abc154_d
E. Almost Everywhere Zero https://atcoder.jp/contests/abc154/tasks/abc154_e
自力 AC. 桁 DP の問題だということをわかった上で解いた。
dp[i][is_less][c] を上位 $i$ 桁目まで見ていて、$N$ よりも小さいことが確定しているフラグ is_less と、0 以外の数字の個数 c を持つ DP 配列を定義する。
dp 配列を更新する際、$0$ 以外の数が $K+1$ となるケースは興味ないので全て $K+1$ に丸めておく。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string N;
ll K;
cin >> N >> K;
int M = N.size();
vector dp(M + 1 , vector(2 , vll(K + 2 )));
dp[0 ][0 ][0 ] = 1 ;
rep2(i, 1 , M + 1 ) {
int t = N[i - 1 ] - '0' ;
rep(d, 10 ) {
int is_not_zero = d != 0 ;
rep(c, 4 ) {
int nxc = min(c + is_not_zero, K + 1 );
if (d < t) {
dp[i][1 ][nxc] += dp[i - 1 ][0 ][c];
}
if (d == t) {
dp[i][0 ][nxc] += dp[i - 1 ][0 ][c];
}
dp[i][1 ][nxc] += dp[i - 1 ][1 ][c];
}
}
}
ll ans = dp[M][1 ][K] + dp[M][0 ][K];
cout << ans << endl;
}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string S;
ll K;
cin >> S >> K;
ll N = S.size();
vector dp(2 , vll(K + 2 ));
dp[0 ][0 ] = 1 ;
rep(i, N) {
int t = S[i] - '0' ;
vector dpn(2 , vll(K + 2 ));
rep(d, 10 ) rep(is_less, 2 ) rep(num_non_zero, K + 1 ) {
if (! is_less && d > t) continue ;
int non_zero = d != 0 ;
int is_less_n = is_less || d < t;
dpn[is_less_n][num_non_zero + non_zero] += dp[is_less][num_non_zero];
}
swap(dp, dpn);
}
cout << dp[0 ][K] + dp[1 ][K] << endl;
}
F. Many Many Paths https://atcoder.jp/contests/abc154/tasks/abc154_f
Mon, Jun 9, 2025 https://atcoder.jp/contests/abc029
A. 複数形 https://atcoder.jp/contests/abc029/tasks/abc029_a
B. カキ https://atcoder.jp/contests/abc029/tasks/abc029_b
C. Brute-force Attack https://atcoder.jp/contests/abc029/tasks/abc029_c
D. 1 https://atcoder.jp/contests/abc029/tasks/abc029_d
自力 AC だが桁 DP の問題ということをわかった上で解いた。
dp[i][is_less][c] を上位 $i$ 桁目までの数を見て $N$ 以下であることが確定(している is_less=1, していない is_less=0)かつ 1 の個数が c 個であるような数の個数とする。
dp[0][0][0] = 1 として、桁を進めていく。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string N;
cin >> N;
int sz = N.size();
int mx = 15 ;
vector dp(sz + 1 , vector(2 , vll(mx)));
dp[0 ][0 ][0 ] = 1 ;
rep2(i, 1 , sz + 1 ) {
int t = N[i - 1 ] - '0' ;
rep(d, 10 ) {
bool is_one = d == 1 ;
rep(c, mx) {
if (d < t) {
dp[i][1 ][c + is_one] += dp[i - 1 ][0 ][c];
}
if (d == t) {
dp[i][0 ][c + is_one] += dp[i - 1 ][0 ][c];
}
dp[i][1 ][c + is_one] += dp[i - 1 ][1 ][c];
}
}
}
ll ans = 0 ;
rep2(c, 1 , mx) { // (N 未満の数で 1 の個数が c 個である数の個数) * c
+= dp[sz][1 ][c] * c;
}
for (char c : N) { // N そのものの 1 の個数を数える
if (c == '1' ) ans++ ;
}
cout << ans << endl;
}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string S;
cin >> S;
ll N = S.size();
int ndigit = 15 ;
// dp[is_less][# of 1]
2 , vll(ndigit));
dp[0 ][0 ] = 1 ;
rep(i, N) {
int t = S[i] - '0' ;
vector dpn(2 , vll(ndigit));
rep(d, 10 ) rep(is_less, 2 ) rep(num, ndigit) {
if (! is_less && d > t) continue ;
int is_less_n = is_less || d < t;
int add = d == 1 ;
dpn[is_less_n][num + add] += dp[is_less][num];
}
swap(dp, dpn);
}
ll ans = 0 ;
rep(num, ndigit) rep(is_less, 2 ) {
ans += dp[is_less][num] * num;
}
cout << ans << endl;
}
Sun, Jun 8, 2025 https://atcoder.jp/contests/abc409
5完で水色パフォーマンスが出たがボンミスや、問題文の誤読などで4ペナもしてしまった。
A - Conflict https://atcoder.jp/contests/abc409/tasks/abc409_a
S[i] == T[i] かだけ調べて o か否かを調べないせいでペナを食らった。
B - Citation https://atcoder.jp/contests/abc409/tasks/abc409_b
$A$ に含まれている要素が答えになると思ったが全部が $10^9$ のとき $x = N$ が答えとなるがそのへんのことが全然考えられていなかった。
$N \leq 100$ で、$A$ に現れるのが $x$ 回以上と言われれば $x \leq N$ となるのは当たり前過ぎたのにそのへんがわかってなくて2ペナもしてしまった。
C - Equilateral Triangle https://atcoder.jp/contests/abc409/tasks/abc409_c
正三角形になるためには $ab$ 間, $bc$ 間, $ca$ 間の距離が等しくなければならず、間隔は $\frac{L}{3}$ である。
$d_i$ が整数なので $L$ が3の倍数でなければ条件と満たすような $a, b, c$ は存在しない。
問題文では点を打つことになっているが該当箇所にコマを置くと考える。
円周を $L$ 分割して 0 から $L-1$ まで点を打つ。$L-1$ の次は 0 に戻る。
$i$ にあるコマの数を $C_i$ とすると求める正三角形の数は
Wed, Jun 4, 2025 A. Divide String https://atcoder.jp/contests/arc163/tasks/arc163_a
自力 AC
文字列の長さは 2 としてよい。
なぜなら $t_1 < t_2 + \cdots + t_k$ であるから。
よって文字列を前半と後半に分割して $t_1 < t_2$ となる分割方法があるか判定すればよい。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
auto cal = []() -> void {
ll N;
string S;
cin >> N >> S;
rep2(i, 1 , N) {
string l = S.substr(0 , i);
string r = S.substr(i, N - i);
if (l < r) {
Yes();
return ;
}
}
No();
};
int t;
cin >> t;
rep(i, t) cal();
}
B. Favorite Game https://atcoder.jp/contests/arc163/tasks/arc163_b
Sun, Jun 1, 2025 https://atcoder.jp/contests/abc408
A. Timeout https://atcoder.jp/contests/abc408/tasks/abc408_a
B. Compression https://atcoder.jp/contests/abc408/tasks/abc408_b
C. Not All Covered https://atcoder.jp/contests/abc408/tasks/abc408_c
D. Flip to Gather https://atcoder.jp/contests/abc408/tasks/abc408_d
コンテスト中に問題文の意味が全く理解できなかった。終了10分前くらいにようやく理解したが結局実装できなかった。
コンテスト終了後2時間近く考えたが結局 AC できなかったのでコンテスト中に問題文の意味が理解できていたとしてもやはり AC できなかっただろう。
解説読んでも理解できなかったのでかなり苦手な問題だったと思う。
解説 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
auto _cal = []() -> void {
int N;
string S;
cin >> N >> S;
// dp[i][j]: i 番目まで決めて末尾がグループ j に属したときの最小コスト
+ 1 , vll(3 , INF));
rep(i, 3 ) dp[0 ][i] = 0 ;
rep2(i, 1 , N + 1 ) {
rep(j, 3 ) {
if (j == 0 ) {
chmin(dp[i][0 ], dp[i - 1 ][0 ] + (ll)(S[i - 1 ] == '1' ));
}
if (j == 1 ) {
chmin(dp[i][1 ], min(dp[i - 1 ][0 ], dp[i - 1 ][1 ]) + (ll)(S[i - 1 ] == '0' ));
}
if (j == 2 ) {
chmin(dp[i][2 ], min(dp[i - 1 ][0 ], min(dp[i - 1 ][1 ], dp[i - 1 ][2 ])) + (ll)(S[i - 1 ] == '1' ));
}
}
}
ll ans = INF;
rep(i, 3 ) chmin(ans, dp[N][i]);
cout << ans << endl;
};
int t;
cin >> t;
rep(i, t) _cal();
}
E. Minimum OR Path https://atcoder.jp/contests/abc408/tasks/abc408_e
Thu, May 29, 2025 A. Digit Sum of 2x https://atcoder.jp/contests/arc144/tasks/arc144_a
自力 AC.
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
ll q = N / 4 ;
ll r = N % 4 ;
string x;
if (r) {
x.push_back('0' + r);
}
rep(i, q) {
x.push_back('4' );
}
ll M = (q * 4 + r) * 2 ;
cout << M << endl;
cout << x << endl;
}
B. Gift Tax https://atcoder.jp/contests/arc144/tasks/arc144_b
WA が取れなかったので解説見たが実装はあっていてなぜ WA したのか特定するのにかなり時間がかかった。
最終的に二分探索するときに使っていた INF として使っている値が大きすぎるのが原因だった。
wa の値を初期値の最大値+1 に抑えれば AC できた。
Thu, May 29, 2025 A. Coprime Pair https://atcoder.jp/contests/arc137/tasks/arc137_a
解説 AC.
解説読んで言わんとすることはわかったが、素数の間隔問題なんて知らないのでどうやっても解ける問題ではなかった。
B. Count 1’s https://atcoder.jp/contests/arc137/tasks/arc137_b
自力 AC
template < typename T>
vector< pair< T, int >> runLengthEncode(const vector< T>& input) {
vector< pair< T, int >> encoded;
int size = input.size();
for (int i = 0 ; i < size; ++ i) {
int count = 1 ;
while (i + 1 < size && input[i] == input[i + 1 ]) {
++ i;
++ count;
}
encoded.emplace_back(input[i], count);
}
return encoded;
}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vint A(N);
rep(i, N) cin >> A[i];
auto ps = runLengthEncode(A);
if (ps.size() == 1 ) {
cout << N + 1 << endl;
return ;
}
int m = ps.size();
int mone = 0 , pone = 0 ;
bool is_init_one = ps[0 ].first == 1 ;
int s0 = 0 , s1 = 1 ;
if (is_init_one) swap(s0, s1);
int sum0 = 0 ;
for (int i = s0; i < m; i += 2 ) {
sum0 += ps[i].second;
chmax(pone, sum0);
if (i + 1 < m) {
sum0 -= ps[i + 1 ].second;
if (sum0 < 0 ) sum0 = 0 ;
}
}
int sum1 = 0 ;
for (int i = s1; i < m; i += 2 ) {
sum1 += ps[i].second;
chmax(mone, sum1);
if (i + 1 < m) {
sum1 -= ps[i + 1 ].second;
if (sum1 < 0 ) sum1 = 0 ;
}
}
int cnt_one = accumulate(all(A), 0 );
int r = cnt_one + pone;
int l = cnt_one - mone;
cout << r - l + 1 << endl;
}
C. Distinct Numbers https://atcoder.jp/contests/arc137/tasks/arc137_c
Wed, May 28, 2025 A. Max Add https://atcoder.jp/contests/arc120/tasks/arc120_a
自力 AC.
$i = 1, 2, \cdots, k$ の順に現在の $a$ の要素の最大値を $a_i$ に足すという操作を操作1と呼ぶことにする。
また $g(a)$ を数列 $a$ に対して操作1を行った後の状態の数列とする。
$a_k = \{A_1, A_2, \cdots, A_k\}$ とし、$f(a_k)$ と $f(a_{k+1})$ との関係性を考える。
$m_k = \max a_k$ とし、$x_k = \max g(a_k)$ とする。
$A_{k+1} \leq m_k$ のとき、操作1の過程で $A_{k+1}$ は $i \in [1, k]$ 番目の操作に影響を及ぼさないため
\begin{align*}
x_{k+1} &= x_k + A_{k+1} \\
f(a_{k+1}) &= f(a_k) + x_{k+1}
\end{align*}
Tue, May 27, 2025 A. Odd vs Even https://atcoder.jp/contests/arc116/tasks/arc116_a
B. Products of Min-Max https://atcoder.jp/contests/arc116/tasks/arc116_b
考えたこと ものすごく複雑なコードになってしまったが自力 AC. 解説放送見たらもっとスマートに解いてた。
$O(N^2)$ 解法であれば数列 $A$ をソートして $i < j$ なる $(i,j)$ の組み合わせに対して $A_i A_j (2^{j-i-1} - 1)$ ひたすら計算して足していく、最後に $A_i^2$ を足せばいいかなと思った。
つまり
\begin{align*}
\sum_{i<j} A_i A_j (2^{j-i-1} - 1) + \sum_{i} A_i^2
\end{align*}
解説はこれをうまいこと変形して計算するスマートな方法でやっていた。
解説のような方法は思いつかなかったので出てくる数字の種類数とその数字の数をもとに考えることにした。
$A$ に含まれる数字が $M$ 種類あるとし、要素を $x_i$ は $x_1 < x_2 < \cdot < x_M$ とし、$x_i$ が現れる個数を $n_i$ とする。
$x_1$ が最小になり、$x_2$ が最大になるような部分集合の個数は、
少なくとも1つの $x_1$ と少なくとも1つの $x_2$ を含む部分集合の個数であるから $(2^{n_1} - 1)(2^{n_2} - 1)$ 通りある。
よって $x_1$ が最小になり、$x_2$ が最大となるような部分集合由来の寄与分は
Sun, May 25, 2025 A. I hate 1 https://atcoder.jp/contests/arc198/tasks/arc198_a
考えたこと
$x$, $x+1$ を選んだ場合は $x+1 \equiv 1 \mod x$ となってしまうため隣接した数字は選べない。
N が $1$ より大きいときに $1$ を入れる他の数字との mod で確実にあまりが1の状況を作れるので入れられない。
そうすると 1 より大きいときは $N, N-2, \cdots$ と選べば良さそうと思ったが WA.
反例として $N=7$ のときに $7, 5, 3$ が選ばれるが $7 \equiv 1 \mod 3$ となってしまうため不適。
全ての要素が偶数であれば何を選んでもあまりが1になることはないし、$\floor{\frac{N}{2}}$ 個の要素を選ぶことができる。隣接する数字を選べないことと 1 が選べないことを考慮するとこれが構築できる最大個数であるから $N \neq 1$ のときは $N$ 以下の偶数を全て選ぶことが最適
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
if (N == 1 ) {
cout << 1 << endl;
cout << 1 << endl;
return ;
}
vint ans;
for (int i = 2 ; i <= N; i += 2 ) {
ans.push_back(i);
}
cout << ans.size() << endl;
print(ans);
}
B. Rivalry https://atcoder.jp/contests/arc198/tasks/arc198_b
Sun, May 25, 2025 https://atcoder.jp/contests/abc407
A. Approximation https://atcoder.jp/contests/abc407/tasks/abc407_a
考えたこと
パット見で方針が立たなくてテンパった。
$|\frac{A}{B} - x|$ を最小化するとき、$|\frac{A - xB}{B}| = \frac{|A - xB|}{B}$ より $|A - xB|$ が最小になるような整数 $x$ を求めれば良さそうと思った。
問題が整数を求めろだったので $x \in [-1000, 1000]$ の範囲で答えを探索するという愚直な方法を取った。
よくよく考えると $A, B$ が正だから負数を考える必要はなかった。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll a, b;
cin >> a >> b;
ll mi = INF;
ll ans = 0 ;
for (ll x = 0 ; x <= 1000 ; x++ ) {
if (abs(a - x * b) < mi) {
ans = x;
mi = abs(a - x * b);
}
}
cout << ans << endl;
}
解説の解説
Fri, May 23, 2025 https://atcoder.jp/contests/abc089
A. Grouping 2 https://atcoder.jp/contests/abc089/tasks/abc089_a
B. Hina Arare https://atcoder.jp/contests/abc089/tasks/abc089_b
C. March https://atcoder.jp/contests/abc089/tasks/abc089_c
D. Practical Skill Test https://atcoder.jp/contests/abc089/tasks/abc089_d
自力 AC
考えたこと $D$ が固定だから経路がかぶるものが出てきそう $R_i$ を $D$ で割った余りが $k$ となる $R_i$ の集合を $G_{k}$ とする $G_{k}$ の中から最大の $R_{\max}$ を選ぶ $L$ から $R$ までの移動で使う魔力の総和を $f(L, R)$ とする $f(R_{\max}, R_{\max})$, $f(R_{\max} - D, R_{\max})$, … を求める $f(L, R) = f(L, R_{\max}) - f(R, R_{\max})$ 累積和で求められそう 解法 「考えたこと」に従った実装したもの。$R_{\max}$ から下っていくことはできるけれど、最小の $L$ の出発点を考えると面倒そうに思えてこの実装になった。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll H, W, D;
cin >> H >> W >> D;
vector A(H, vll(W));
rep(i, H) rep(j, W) {
cin >> A[i][j];
A[i][j]-- ;
}
vector< pair< int , int >> num_pos(H * W);
rep(i, H) rep(j, W) num_pos[A[i][j]] = {i, j};
int Q;
cin >> Q;
vector< pair< int , int >> queries;
rep(i, Q) {
int l, r;
cin >> l >> r;
l-- , r-- ;
queries.emplace_back(l, r);
}
vint rmax(D, 0 );
vector< bool > rexists(D, 0 );
for (auto [l, r] : queries) {
chmax(rmax[r % D], r);
rexists[r % D] = true;
}
map< pair< int , int > , ll> memo;
auto f = [& ](auto f, int l, int r) -> ll {
if (l == r)
return 0 ;
auto [ni, nj] = num_pos[l + D];
auto [i, j] = num_pos[l];
return memo[{l, r}] = abs(ni - i) + abs(nj - j) + f(f, l + D, r);
};
rep(i, D) {
if (! rexists[i])
continue ;
f(f, i, rmax[i]);
}
for (auto [l, r] : queries) {
int rmx = rmax[r % D];
cout << memo[{l, rmx}] - memo[{r, rmx}] << '\n' ;
}
}
解説見て直した実装。最小の $L$ は単純に $0 \sim D-1$ 出発で考えればいいだけだった。
Thu, May 22, 2025 https://atcoder.jp/contests/abc262
A. World Cup https://atcoder.jp/contests/abc262/tasks/abc262_a
B. Triangle (Easier) https://atcoder.jp/contests/abc262/tasks/abc262_b
C. Min Max Pair https://atcoder.jp/contests/abc262/tasks/abc262_c
D. I Hate Non-integer Number https://atcoder.jp/contests/abc262/tasks/abc262_d
自力 AC
考えたこと 平均が整数になるということは $k$ 個を選んだとしたら選んだ数の和が $k$ で割り切れるということ $a_i$ を $k$ で割った余りを求めてそれらから $k$ 個を選んだときの和の余りが $0$ になる組み合わせの数を求めれば良い dp が使えそう$i$ 番目までの要素を見たときに $j$ 個を選んだときの和の余りが $m$ になる組み合わせは dp で求められる 全ての $k$ について求めて足し合わせる $N \leq 100$ だから $O(N^4)$ でも間に合う 解法 $a_i$ を $d \in [1, N]$ で割った余りを予め求めておいて、その中から $d$ 個を選んだ和を $d$ で割った余りが $0$ となる組み合わせの数を求める。
これを全ての $d$ について求めて足し合わせる。
Wed, May 21, 2025 https://atcoder.jp/contests/abc353
A. Buildings https://atcoder.jp/contests/abc353/tasks/abc353_a
B. AtCoder Amusement Park https://atcoder.jp/contests/abc353/tasks/abc353_b
C. Sigma Problem https://atcoder.jp/contests/abc353/tasks/abc353_c
D. Another Sigma Problem https://atcoder.jp/contests/abc353/tasks/abc353_d
E. Yet Another Sigma Problem https://atcoder.jp/contests/abc353/tasks/abc353_e
$0 \sim i-1$ 文字目が同じで $i$ 文字目も同じであるような文字列の数が $N_i$ 個あったとすると、$i$ 文字目の寄与は $\binom{N_i}{2}$ である。
Trie を使って、これらの個数を数える。各ノードの共有している文字列の数は入力例2では以下のようになる。
\begin{align*}
&\binom{6}{2} + \binom{3}{2} + \binom{2}{2} + \binom{5}{2} + \binom{2}{2} + \binom{2}{2} + \binom{2}{2} \\
&= 15 + 3 + 1 + 10 + 1 + 1 + 1 \\
&= 32
\end{align*}
Tue, May 20, 2025 https://atcoder.jp/contests/abc299
A. Treasure Chest https://atcoder.jp/contests/abc299/tasks/abc299_a
B. Trick Taking https://atcoder.jp/contests/abc299/tasks/abc299_b
C. Dango https://atcoder.jp/contests/abc299/tasks/abc299_c
D. Find by Query https://atcoder.jp/contests/abc299/tasks/abc299_d
E. Nearest Black Vertex https://atcoder.jp/contests/abc299/tasks/abc299_e
BFS を使って、各頂点間の最短距離をまずは求める。
一旦全ての頂点を黒く塗る。
次に、各頂点 p から d より近いところにある黒を白く塗り直す。
その後、各頂点について条件を満たす黒い頂点があるか調べる。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, M;
cin >> N >> M;
vvint graph(N);
rep(i, M) {
int u, v;
cin >> u >> v;
u-- , v-- ;
graph[u].push_back(v);
graph[v].push_back(u);
}
int K;
cin >> K;
vector< pair< int , int >> ps;
rep(i, K) {
int p, d;
cin >> p >> d;
p-- ;
ps.push_back({p, d});
}
auto short_path = [](vvint& graph, int start) -> vint {
int N = graph.size();
vint dist(N, INF);
dist[start] = 0 ;
// cost, position
using P = pair< ll, int > ;
deque< P> deq;
deq.push_back({0 , start});
while (deq.size()) {
auto [cost, now] = deq.front();
deq.pop_front();
if (dist[now] < cost)
continue ;
for (int nx : graph[now]) {
if (dist[nx] <= cost + 1 )
continue ;
dist[nx] = cost + 1 ;
deq.push_back({cost + 1 , nx});
}
}
return dist;
};
vvint dists(N);
rep(i, N) {
dists[i] = short_path(graph, i);
}
// 一旦全ての頂点を黒く塗る
1 );
// 頂点 p から d より近いところにある黒を白く塗り直す
for (auto [p, d] : ps) {
rep(i, N) {
if (dists[p][i] < d)
black[i] = 0 ;
}
}
// 各頂点について条件を満たす黒い頂点があるか調べる
for (auto [p, d] : ps) {
int ok = 0 ;
rep(i, N) {
if (dists[p][i] == d && black[i])
ok = 1 ;
}
if (! ok) {
yesno(false);
return ;
}
}
yesno(true);
for (int x : black)
cout << x;
cout << endl;
}
F. Square Subsequence https://atcoder.jp/contests/abc299/tasks/abc299_f
Mon, May 19, 2025 A. B = C https://atcoder.jp/contests/arc112/tasks/arc112_a
B. – - B https://atcoder.jp/contests/arc112/tasks/arc112_b
自力 AC.
解説放送と同じ方式
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll B, C;
cin >> B >> C;
vector< pair< ll, ll>> ps;
ps.emplace_back(B - C / 2 , B + (C - 2 ) / 2 );
ps.emplace_back(- B - (C - 1 ) / 2 , - B + (C - 1 ) / 2 );
sort(all(ps));
if (ps[0 ].second >= ps[1 ].first) {
ps[0 ].second = ps[1 ].second;
ps.pop_back();
}
ll ans = 0 ;
for (auto [x, y] : ps) {
ans += y - x + 1 ;
}
cout << ans << endl;
}
C. DFS Game https://atcoder.jp/contests/arc112/tasks/arc112_c
Sun, May 18, 2025 https://atcoder.jp/contests/abc406
B - Product Calculator 多倍長整数の問題を C++ で解くと時間がかかりそうだったので、コンテスト中は Python で解いた
$a$, $X$, $Y$ が整数のとき、$aX > Y \Leftrightarrow X > \floor{\frac{Y}{a}}$ となるので $Y = 10^K - 1$, $X$ を表示されている数としたとき、$X > \floor{\frac{Y}{a}}$ なら $X = 1$ とし、そうでないならば $X$ に $a$ を掛ける。
def main ():
n, k = map(int, input(). split())
a = map(int, input(). split())
mx = 10 ** k
ans = 1
for i in a:
ans *= i
if ans >= mx:
ans = 1
print(ans)
main()
ll intpow (ll x, ll n) {
long long ret = 1 ;
while (n > 0 ) {
if (n & 1 )
ret *= x;
x *= x;
n >>= 1 ;
}
return ret;
}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, K;
cin >> N >> K;
vll A(N);
rep(i, N) cin >> A[i];
ll mx = intpow(10 , K) - 1 ;
ll ans = 1 ;
for (ll a : A) {
if (ans > mx / a) {
ans = 1 ;
} else {
ans *= a;
}
}
cout << ans << endl;
}
C - ~ /\/\/... といった形のように数字が上下振れているところから /\/ の部分に着目して個数を数えていく。
Sat, May 17, 2025 https://atcoder.jp/contests/past202005-open
H - ハードル走 自力 AC.
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, L;
cin >> N >> L;
vll X(N);
rep(i, N) cin >> X[i];
ll T1, T2, T3;
cin >> T1 >> T2 >> T3;
vll hurdles(L + 1 );
for (ll x : X)
hurdles[x] = 1 ;
vll dp(L + 1 , INF);
dp[0 ] = 0 ;
rep2(i, 1 , L + 1 ) {
ll offset = hurdles[i] * T3;
chmin(dp[i], dp[i - 1 ] + T1 + offset);
if (i - 2 >= 0 ) {
chmin(dp[i], dp[i - 2 ] + T1 + T2 + offset);
}
if (i - 4 >= 0 ) {
chmin(dp[i], dp[i - 4 ] + T1 + T2 * 3 + offset);
}
// ジャンプして超える
if (i == L) {
if (i - 3 >= 0 ) {
chmin(dp[i], dp[i - 3 ] + T1 / 2 + T2 / 2 * 5 );
}
if (i - 2 >= 0 ) {
chmin(dp[i], dp[i - 2 ] + T1 / 2 + T2 / 2 * 3 );
}
if (i - 1 >= 0 ) {
chmin(dp[i], dp[i - 1 ] + T1 / 2 + T2 / 2 );
}
}
}
cout << dp[L] << endl;
}
Fri, May 16, 2025 A. Yet Another AB Problem https://atcoder.jp/contests/arc170/tasks/arc170_a
B. Arithmetic Progression Subsequence https://atcoder.jp/contests/arc170/tasks/arc170_b
解説 AC.
以下のサイトを見て理論は理解したが、$O(NM^2)$ 解法の等差数列判定の部分が理解できなかった。
https://ikatakos.com/pot/programming_algorithm/contest_history/atcoder/2024/0121_arc170
$O(NM^4)$ 解法であれば解けた。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vint A(N);
rep(i, N) cin >> A[i];
auto is_seq = [& ](int l, int r) -> bool {
bool ok = false;
r++ ;
rep2(i, l, r) {
rep2(j, i + 1 , r) {
rep2(k, j + 1 , r) {
if (A[j] - A[i] == A[k] - A[j])
ok = true;
}
}
}
return ok;
};
ll ans = N * (N + 1 ) / 2 ;
rep(l, N) {
rep2(r, l, N) {
if (is_seq(l, r)) {
break ;
} else {
ans-- ;
}
}
}
cout << ans << endl;
}
C. Prefix Mex Sequence https://atcoder.jp/contests/arc170/tasks/arc170_c
Wed, May 14, 2025 A. 2nd Greatest Distance https://atcoder.jp/contests/arc121/tasks/arc121_a
B. RGB Matching https://atcoder.jp/contests/arc121/tasks/arc121_b
赤の個数を $N_R$、緑の個数を $N_G$、緑の個数を $N_B$ とする。
$N_R + N_G + N_B \equiv 0 \mod 2$ より、3つの数の組み合わせは偶数3つ、または、奇数2つと偶数1つである。
全て偶数のときは同じ色同士で組を作れば良いから不満の総和は 0 である。
以降、赤と緑の個数が奇数となり、青の個数が偶数とする。
このとき、以下の2パターンが考えられる。
赤と緑で1つ組を作り、それ以外は同じ色同士で組を作る 赤と青で1つ、緑と青で1つ組を作り、それ以外は同じ色同士で組を作る 2パターンのうちの不満の総和が最小のほうが答え。
(1) のとき、差が一番小さいようなものを調べればよい。
(2) のとき、$r_i$ を $i$ 番目の青と組を作ったときに一番不満が小さくなるように赤を選んだときの不満の値とする。
同様に緑に対して $g_i$ を定義する。
$dp(i, state)$ を青を $i$ 番目まで見て $state$ 状態になったときの不満の総和の最小値とする。
ここで $state$ は以下のように定義する。
$state=1$: 赤とペアを組む青が決まっている $state=2$: 緑とペアを組む青が決まっている $state=3$: 赤と緑とペアを組む青が決まっている \begin{align*}
dp(i, 1) &= \min(dp(i-1, 1), r_i) \\
dp(i, 2) &= \min(dp(i-1, 2), g_i) \\
dp(i, 3) &= \min(r_i + dp(i-1, 2), g_i + dp(i-1, 1), dp(i-1, 3))
\end{align*}
Tue, May 13, 2025 https://atcoder.jp/contests/abc058
A. Make it Zigzag https://atcoder.jp/contests/agc058/tasks/agc058_a
0-index で考える。
$i \equiv 0 \mod 2$ のときに、$P_i$, $P_{i+1}$, $P_{i+2}$ の大小関係は以下の4通りにに分けられる。
Type A: $P_i < P_{i+1} < P_{i+2}$ Type B: $P_i > P_{i+1} > P_{i+2}$ Type C: $P_i > P_{i+1} < P_{i+2}$ Type D: $P_i < P_{i+1} > P_{i+2}$ Type A のとき、
$\mathrm{swap}(P_{i+1}, P_{i+2})$ を行うことで $P_i < P_{i+1} > P_{i+2}$ を実現できる
Type B のとき、
$\mathrm{swap}(P_i, P_{i+1})$ を行うことで $P_i < P_{i+1} > P_{i+2}$ を実現できる
Type C のとき、
$P_i > P_{i+2}$ ならば $\mathrm{swap}(P_i, P_{i+1})$ を行い、$P_i < P_{i+2}$ なら $\mathrm{swap}(P_{i+1}, P_{i+2})$ をすることで $P_i < P_{i+1} > P_{i+2}$ を実現できる
Mon, May 12, 2025 A. Ekiden Race https://atcoder.jp/contests/arc162/tasks/arc162_a
人 $i$ が順位下げた場合、人 $i$ よりも早く走った人がいることになるので復路でのタイムが最も早かったことにはならない。
また順位を下げていなくても以下の図1 の Y のように誰かに抜かされていたらその人も復路でのタイムが最も早かったことにはならない。
これらの人を除くと位置関係は図2 のように往路、往復での相対的な位置関係が変わらない人だけが残る。
これらの人の復路でのタイムが同じでも位置関係は保たれるのでこのような条件を満たす人たちの数を数えれば良い。
位置関係
図1
┌──────────────────┐
│ │
│ ▼
X Y Z────►Z Y X
│ ▲
│ │
└───────────┘
図2
┌───────────┐
│ │
│ ▼
X Y X Y
│ ▲
│ │
└───────────┘
┌──────┐
│ │
│ ▼
X X Y Y
│ ▲
│ │
└─────┘
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
auto cal = []() -> void {
ll N;
cin >> N;
vll P(N);
rep(i, N) cin >> P[i];
vector< pair< ll, ll>> ps;
rep(i, N) {
ps.emplace_back(i + 1 , P[i]);
}
reverse(all(ps));
ll l = - 1 , r = INF;
ll ans = 0 ;
for (auto [before, after] : ps) {
if (before < after) continue ;
if (before < l && r < after) continue ;
ans++ ;
l = before, r = after;
}
cout << ans << '\n' ;
};
int t;
cin >> t;
rep(i, t) cal();
}
B. Insertion Sort 2 https://atcoder.jp/contests/arc162/tasks/arc162_b
Sun, May 11, 2025 https://atcoder.jp/contests/abc405
D - Escape Route まず複数ある非常口から通路マスへの距離の最短を求める。
マス $(i,j)$ から隣のマスへの距離が -1 のとき、その方向に進む記号を記録して出力する。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll H, W;
cin >> H >> W;
vector< string> grid(H);
rep(i, H) cin >> grid[i];
int si = 0 , sj = 0 ;
vector< pair< int , int >> exits;
rep(i, H) rep(j, W) {
if (grid[i][j] == 'E' )
exits.push_back({i, j});
}
// i,j, cost
deque< tuple< ll, ll, ll>> deq;
for (auto [i, j] : exits) {
deq.push_back({i, j, 0 });
dist[i][j] = 0 ;
}
vll di = {0 , 1 , 0 , - 1 };
vll dj = {1 , 0 , - 1 , 0 };
while (deq.size()) {
auto [nowi, nowj, cost] = deq.front();
deq.pop_front();
if (dist[nowi][nowj] < cost)
continue ;
rep(dir, 4 ) {
ll ni = nowi + di[dir], nj = nowj + dj[dir];
if (clamp(ni, 0ll , H - 1 ) != ni || clamp(nj, 0ll , W - 1 ) != nj)
continue ;
if (grid[ni][nj] == '#' )
continue ;
if (dist[ni][nj] <= cost + 1 )
continue ;
dist[ni][nj] = cost + 1 ;
deq.push_back({ni, nj, dist[ni][nj]});
}
}
vector< char > dir_mark = {'>' , 'v' , '<' , '^' };
vector< string> ans = grid;
rep(i, H) {
rep(j, W) {
if (grid[i][j] == '#' || grid[i][j] == 'E' )
continue ;
rep(dir, 4 ) {
ll ni = i + di[dir], nj = j + dj[dir];
if (clamp(ni, 0ll , H - 1 ) != ni || clamp(nj, 0ll , W - 1 ) != nj)
continue ;
if (dist[i][j] == dist[ni][nj] + 1 ) {
ans[i][j] = dir_mark[dir];
}
}
}
}
for (auto s : ans)
cout << s << endl;
}
E - Fruit Lineup 解説 AC
Sat, May 10, 2025 A. Replace C or Swap AB https://atcoder.jp/contests/arc166/tasks/arc166_a
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
auto check = [](string X, string Y) -> bool {
int n = X.size();
int xa = 0 , ya = 0 ;
for (char c : X) {
if (c == 'A' )
xa++ ;
}
for (char c : Y) {
if (c == 'A' )
ya++ ;
}
if (xa > ya)
return false;
int rema = ya - xa;
rep(i, n) {
if (X[i] == 'C' ) {
if (rema) {
X[i] = 'A' ;
rema-- ;
} else {
X[i] = 'B' ;
}
}
}
set< int > xbpos;
rep(i, n) {
if (X[i] == 'B' )
xbpos.insert(i);
}
rep(i, n) {
if (X[i] == Y[i])
continue ;
if (X[i] == 'B' && Y[i] == 'A' )
return false;
if (X[i] == 'A' && Y[i] == 'B' ) {
auto it = xbpos.lower_bound(i);
if (it == xbpos.end())
return false;
swap(X[i], X[* it]);
xbpos.erase(it);
}
}
return true;
};
auto cal = [& ]() -> void {
int N;
string X, Y;
cin >> N >> X >> Y;
if (X == Y) {
yesno(true);
return ;
}
// sentinel
'C' );
Y.push_back('C' );
N++ ;
int start = 0 ;
rep(i, N) {
if (Y[i] == 'C' && X[i] != 'C' ) {
yesno(false);
return ;
}
if (X[i] == 'C' && Y[i] == 'C' ) {
int len = i - start;
if (! check(X.substr(start, len), Y.substr(start, len))) {
yesno(false);
return ;
};
start = i + 1 ;
continue ;
}
}
yesno(true);
};
int t;
cin >> t;
rep(i, t) {
cal();
}
}
B. Make Multiples https://atcoder.jp/contests/arc166/tasks/arc166_b
Tue, May 6, 2025 A. 119 × 2^23 + 1 https://atcoder.jp/contests/arc119/tasks/arc119_a
B. Electric Board https://atcoder.jp/contests/arc119/tasks/arc119_b
解説 AC.
1 を基準に動かすことを考えていたが、0 を基準に動かすことを考えるべきだったらしい。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
string S, T;
cin >> S >> T;
vint s, t;
rep(i, N) {
if (S[i] == '0' )
s.push_back(i);
if (T[i] == '0' )
t.push_back(i);
}
if (s.size() != t.size()) {
cout << - 1 << endl;
return ;
}
int ans = 0 ;
rep(i, s.size()) {
if (s[i] != t[i])
ans++ ;
}
cout << ans << endl;
}
C. ARC Wrecker 2 https://atcoder.jp/contests/arc119/tasks/arc119_c
Mon, May 5, 2025 A. Tax Included Price https://atcoder.jp/contests/arc118/tasks/arc118_a
B. Village of M People https://atcoder.jp/contests/arc118/tasks/arc118_b
解説 AC.
二分探索を使って upper bound を探索するところまでは思いついたが、$B$ を構築できるかの判定が甘くて自力で AC できなかった。
$\max_i |\frac{B_i}{M} - \frac{A_i}{N}| = \frac{1}{MN} \max_i | NB_i - MA_i |$ より $\max_i | NB_i - MA_i |$ の最小化問題に帰着できる。
$\max_i | NB_i - MA_i | \leq D$ となる $D$ が存在するとき
\begin{align*}
-D \leq NB_i - MA_i \leq D \\
-D + MA_i \leq NB_i \leq D + MA_i \\
\frac{-D + MA_i}{N} \leq B_i \leq \frac{D + MA_i}{N}
\end{align*}
Sat, May 3, 2025 https://atcoder.jp/contests/abc404
B - Grid Rotation 90度回転を 0 ~ 3 回行い、それぞれのときの色が違うマスの数 + 回転回数が答え。
配列を90度回転させるところが一番難しい。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vector< string> S(N), T(N);
rep(i, N) cin >> S[i];
rep(i, N) cin >> T[i];
auto rotr90 = [& ](vector< string>& S) -> vector< string> {
vector< string> newS = S;
rep(i, N) {
rep(j, N) {
// newS[j][N - 1 - i] = S[i][j];
= S[N - j - 1 ][i];
}
}
return newS;
};
ll ans = INF;
rep(k, 4 ) {
if (k)
S = rotr90(S);
ll cnt = k;
rep(i, N) rep(j, N) {
if (S[i][j] != T[i][j])
cnt++ ;
}
chmin(ans, cnt);
}
cout << ans << endl;
}
C - Cycle Graph? union find で実装しようとして2ペナを食らった。union find で実装する場合は連結であることと、全てのノードの次数が2であることを確認する必要があった。
コンテスト中は union find 解法が思いつかなかったので dfs で実装した。
Fri, May 2, 2025 A. Ternary Decomposition https://atcoder.jp/contests/arc164/tasks/arc164_a
自力 AC.
$N$ を3進数で表現したとき、すなわち $N = \sum_{i=0}^m c_i 3^i$ と展開したとき $\sum_i c_i$ が $N$ を 3 の冪乗のみで構成したときの項の個数の最小値である。
ここで $n > 0$ のとき $3^n = 3^{n-1} + 3^{n-1} + 3^{n-1}$ とできるので1項を3項に分解できる。
すなわち、1つの項を分解すると項数は $+2$ される。
現時点での項数を $S$ とする。
$3^n$ を $x$ を分解すると $2x$ 個項数が増えるので、分解すべき最大の個数は
\begin{align*}
S + 2x &\leq K \\
x &\leq \frac{K - S}{2} \\
x &\leq \floor{\frac{K - S}{2}}
\end{align*}
となる。
Thu, May 1, 2025 https://atcoder.jp/contests/abc208
A. Rolling Dice https://atcoder.jp/contests/abc208/tasks/abc208_a
B. Factorial Yen Coin https://atcoder.jp/contests/abc208/tasks/abc208_b
C. Fair Candy Distribution https://atcoder.jp/contests/abc208/tasks/abc208_c
D. Shortest Path Queries 2 https://atcoder.jp/contests/abc208/tasks/abc208_d
ワーシャルフロイドの一番外側の loop が経由地を増やしていることと同義なので、$(A, B)$ 間の距離を更新しつつ、距離が $\infty$ でなければ加算していくことを繰り返せばよい。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, M;
cin >> N >> M;
vector dist(N, vll(N, INF));
rep(i, M) {
ll u, v, c;
cin >> u >> v >> c;
u-- , v-- ;
dist[u][v] = c;
}
rep(i, N) dist[i][i] = 0 ;
ll ans = 0 ;
rep(k, N) {
rep(i, N) {
rep(j, N) {
if (dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
if (dist[i][j] != INF) {
ans += dist[i][j];
}
}
}
}
cout << ans << endl;
}
E. Digit Products https://atcoder.jp/contests/abc208/tasks/abc208_e
Thu, May 1, 2025 https://atcoder.jp/contests/abc193
A. Discount https://atcoder.jp/contests/abc193/tasks/abc193_a
B. Play Snuke https://atcoder.jp/contests/abc193/tasks/abc193_b
C. Unexpressed https://atcoder.jp/contests/abc193/tasks/abc193_c
D. Poker https://atcoder.jp/contests/abc193/tasks/abc193_d
愚直に確率を計算するだけ。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll K;
string S, T;
cin >> K >> S >> T;
vll cnt(10 , K);
rep(i, 4 ) {
cnt[S[i] - '0' ]-- ;
cnt[T[i] - '0' ]-- ;
}
auto score = [& ](string s) -> ll {
vll used(10 );
for (char c : s)
used[c - '0' ]++ ;
ll ans = 0 ;
rep2(i, 1 , 10 ) {
ans += i * intpow(10 , used[i]);
}
return ans;
};
ll ans = 0 ;
S[4 ] = T[4 ] = '0' ;
rep2(i, 1 , 10 ) {
rep2(j, 1 , 10 ) {
S.back() = '0' + i;
T.back() = '0' + j;
if (score(S) <= score(T))
continue ;
ans += cnt[i] * (cnt[j] - (i == j));
}
}
ll rem = K * 9 - 8 ;
printf("%.9lf \n " , (double )ans / (double )(rem * (rem - 1 )));
}
E. Oversleeping https://atcoder.jp/contests/abc193/tasks/abc193_e
Wed, Apr 30, 2025 https://atcoder.jp/contests/abc277
A. ^{-1} https://atcoder.jp/contests/abc277/tasks/abc277_a
B. Playing Cards Validation https://atcoder.jp/contests/abc277/tasks/abc277_b
C. Ladder Takahashi https://atcoder.jp/contests/abc277/tasks/abc277_c
D. Takahashi’s Solitaire https://atcoder.jp/contests/abc277/tasks/abc277_d
E. Crystal Switches https://atcoder.jp/contests/abc277/tasks/abc277_e
12 min で AC
類題: https://atcoder.jp/contests/abc395/tasks/abc395_e
$a_i = 0$ の辺で構成される sub graph を $G$, $a_i = 1$ の辺で構成される sub graph を $G^\prime$ とする。
このとき、辺 $(u, v)$ は $G^\prime$ 上では $(u+N, v+N)$ として扱う。
スイッチがある頂点 $x$ には頂点 $x+N$ との間にコスト 0 の辺を張り、それ以外の辺はコスト 1 としてダイクストラを実行する。
頂点 $N$, $2N$ のコストのうち最小を出力する。どちらの頂点にも到達できない場合は -1 を出力する。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, M, K;
cin >> N >> M >> K;
vector< tuple< int , int , int >> es;
rep(i, M) {
int u, v, a;
cin >> u >> v >> a;
u-- , v-- ;
es.emplace_back(u, v, a);
}
vector< bool > sw(N);
rep(i, K) {
int s;
cin >> s;
s-- ;
sw[s] = true;
}
vvint graph(N * 2 );
for (auto [u, v, a] : es) {
if (a == 1 ) {
graph[u].push_back(v);
graph[v].push_back(u);
} else {
graph[u + N].push_back(v + N);
graph[v + N].push_back(u + N);
}
if (sw[u]) {
graph[u].push_back(u + N);
graph[u + N].push_back(u);
}
if (sw[v]) {
graph[v].push_back(v + N);
graph[v + N].push_back(v);
}
}
vll dists(N * 2 , INF);
dists[0 ] = 0 ;
// cost, position
< pair< ll, ll>> dq;
dq.push_back({0 , 0 });
while (dq.size()) {
auto [cost, now] = dq.front();
dq.pop_front();
if (dists[now] < cost)
continue ;
for (int nx : graph[now]) {
ll d = cost;
int add = 0 ;
if (abs(nx - now) != N) {
d++ ;
add++ ;
}
if (dists[nx] <= d)
continue ;
dists[nx] = d;
if (add)
dq.push_back({d, nx});
else
dq.push_front({d, nx});
}
}
ll ans = INF;
chmin(ans, dists[N - 1 ]);
chmin(ans, dists[N * 2 - 1 ]);
if (ans == INF)
ans = - 1 ;
cout << ans << endl;
}
F. Sorting a Matrix https://atcoder.jp/contests/abc277/tasks/abc277_f
Mon, Apr 28, 2025 https://atcoder.jp/contests/abc403
A. Odd Position Sum https://atcoder.jp/contests/abc403/tasks/abc403_a
B. Four Hidden https://atcoder.jp/contests/abc403/tasks/abc403_b
C. 403 Forbidden https://atcoder.jp/contests/abc403/tasks/abc403_c
D. Forbidden Difference https://atcoder.jp/contests/abc403/tasks/abc403_d
index の情報は重要ではなく数の出現頻度が重要なのでまずはそれを調べる。
$D=0$ のとき 数 $x$ の頻度が $C_x$ のとき、$x$ を1つ残すのが最適なので削除する個数は $C_x - 1$ 個。これを出現する全ての数に対して足し合わせたものが答え。
$D>0$ のとき $D$ 離れている数をグルーピングして DP を行う。
配列 $B$ に $x$ の出現頻度を格納する。
$dp_{i,j}$ を $j$ 番目の数を $i=1$ のときは削除する、$i=0$ のときは削除しないときの、$1~j$ までの数を削除した最小の個数とすると
\begin{align*}
dp_{0,j} &= dp_{1,j-1} \\
dp_{1,j} &= \min(dp_{0,j-1}, dp_{1,j-1}) + B_{j}
\end{align*}
となる。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, D;
cin >> N >> D;
vll A(N);
rep(i, N) cin >> A[i];
if (D == 0 ) {
ll ans = 0 ;
map< ll, ll> cnt;
for (ll x : A)
cnt[x]++ ;
for (auto [k, v] : cnt) {
ans += v - 1 ;
}
cout << ans << endl;
return ;
}
map< ll, ll> cnts;
for (ll x : A)
cnts[x]++ ;
ll ans = 0 ;
set< int > used;
for (auto [k, v] : cnts) {
if (used.count(k))
continue ;
vll B = {v};
used.insert(k);
ll t = k;
while (cnts.count(t + D)) {
t += D;
B.push_back(cnts[t]);
used.insert(t);
}
// dp[i][j] : i 1 捨てる, 0 捨てない
// j 個目の数に対して
2 , vll(B.size() + 1 , INF));
dp[0 ][0 ] = dp[1 ][0 ] = 0 ;
rep2(i, 1 , B.size() + 1 ) {
dp[0 ][i] = dp[1 ][i - 1 ]; // i 番目を採用する場合は i-1 番目は削除する必要がある
1 ][i] = min(dp[0 ][i - 1 ], dp[1 ][i - 1 ]) + B[i - 1 ]; // i 番目を削除する場合は i-1 番目は削除してもしなくてもどっちでもいい
ans += min(dp[0 ][B.size()], dp[1 ][B.size()]);
}
cout << ans << endl;
}
コンテスト中は出現しない数に対しては DP の対象にしなかったが、出現しない数も頻度が 0 として扱えば $\mod D$ 毎にグルーピングして DP するという風にできた
Fri, Apr 25, 2025 A. Please Sign https://atcoder.jp/contests/arc169/tasks/arc169_a
解説 AC
こちらの動画を見て理解した
https://youtu.be/A79qGX7OFMM?si=PPJI_IB_vRbaFFaZ
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vll A(N);
rep(i, N) cin >> A[i];
vint depth(N);
vll B(N);
B[0 ] = A[0 ];
rep2(i, 1 , N) {
int p;
cin >> p;
p-- ;
depth[i] = depth[p] + 1 ;
B[depth[i]] += A[i];
}
string ans = "0" ;
for (int i = N - 1 ; i >= 0 ; i-- ) {
if (B[i] == 0 )
continue ;
if (B[i] < 0 )
ans = "-" ;
if (B[i] > 0 )
ans = "+" ;
break ;
}
cout << ans << endl;
}
B. Subsegments with Small Sums https://atcoder.jp/contests/arc169/tasks/arc169_b
Sun, Apr 20, 2025 https://atcoder.jp/contests/abc402
C - Dislike Foods 食材 $i$ を使用している料理の番号、料理 $j$ が使用している苦手な食材の数をそれぞれ保存しておく。
食材 $B_i$ を克服したとき、料理 $j$ が食材 $B_i$ を使用していたら、料理 $j$ の苦手な食材の数を1減らす。苦手な食材の数が 0 になったら食べられる料理の個数を1増やす。
これを繰り返す
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, M;
cin >> N >> M;
vvll A(M);
rep(i, M) {
int K;
cin >> K;
rep(j, K) {
ll a;
cin >> a;
a-- ;
A[i].push_back(a);
}
}
vll B(N);
rep(i, N) {
cin >> B[i];
B[i]-- ;
}
// shokuzai[i]: 食材 i を使っている料理の番号
rep(i, M) {
for (ll a : A[i]) {
shokuzai[a].push_back(i);
}
}
// nums[i]: 料理 i に含まれる苦手な食材の数
0 );
rep(i, M) nums[i] = A[i].size();
ll ans = 0 ;
for (ll b : B) {
for (ll i : shokuzai[b]) {
nums[i]-- ;
if (nums[i] == 0 )
ans++ ;
}
cout << ans << endl;
}
}
D - Line Crossing AC したが、実験して多分これで通るんじゃないかなぁくらいののりで提出して AC した。
Wed, Apr 16, 2025 https://atcoder.jp/contests/past17-open
H - 履修登録 解説 AC.
dp[i][j] を $i$ 限目までの科目をこなして $j$ 単位取得するのに必要な最小の労力とする。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll n, m;
cin >> n >> m;
vll a(n), b(n), c(n);
rep(i, n) cin >> a[i] >> b[i] >> c[i];
vector< vector< pair< ll, ll>>> lec(5001 );
rep(i, n) {
lec[b[i]].push_back({a[i], c[i]});
}
vvll dp(5001 , vll(m + 1 , INF));
dp[0 ][0 ] = 0 ;
rep2(i, 1 , 5001 ) {
rep(j, m + 1 ) {
// i 限目の科目を取らない場合
- 1 ][j]);
// i 限目の科目を取る場合
chmin(dp[i][j], dp[i - 1 ][max(0ll , j - lec[i][k].second)] + lec[i][k].first);
}
}
}
ll ans = dp[5000 ][m];
if (ans == INF)
ans = - 1 ;
cout << ans << endl;
}
K - 正しいチェックディジット https://atcoder.jp/contests/past17-open/tasks/past17_k
Wed, Apr 16, 2025 https://atcoder.jp/contests/past18-open
G - 二回の交換 $A = B$ のとき、$A_1, A_2$ を交換する操作を2回行えば良い。
$A \neq B$ のときを考える。
交換操作を行うする左端の index として $i < j$ なる $i,j$ を選ぶ。
このとき $(A_i, A_{i+1})$ の交換と $(A_j, A_{j+1})$ の交換操作は一般に非可換である。
一方で今回の問題では交換回数が2回なので次の2通りの置換のみ考えれば十分である。
\begin{eqnarray*}
\begin{pmatrix}
1 & 2 & 3 \\
3 & 1 & 2
\end{pmatrix}
\begin{pmatrix}
1 & 2 & 3 \\
2 & 3 & 1
\end{pmatrix}
\end{eqnarray*}
題意を満たすような操作方法は以下の3通りである
(1) $i$ が小さい方から処理していき $A_i \neq B_i$ なる部分があれば $(A_i, A_{i+1})$ を交換する操作を繰り返し操作回数が2回かつ、最終的に $A = B$ となる (2) $i$ が大きい方から処理しておき $A_i \neq B_i$ なる部分があれば $(A_{i-1}, A_{i})$ を交換する操作を繰り返し操作回数が2回かつ、最終的に $A = B$ となる (3) 一度の交換で $A = B$ となり、かつ、操作前または操作後の数列において同じ数字が連続している部分が存在している (2) に関しては数列を反転させて (1) と同じ操作を行えば良い。
Sat, Apr 12, 2025 https://atcoder.jp/contests/abc401
D - Logical Filling https://atcoder.jp/contests/abc401/tasks/abc401_d
解説 AC
vector< pair< char , int >> runLengthEncode(const string& input) {
vector< pair< char , int >> encoded;
int size = input.size();
for (int i = 0 ; i < size; ++ i) {
int count = 1 ;
while (i + 1 < size && input[i] == input[i + 1 ]) {
++ i;
++ count;
}
encoded.emplace_back(input[i], count);
}
return encoded;
}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, K;
string S;
cin >> N >> K >> S;
rep(i, N) {
if (i + 1 < N && S[i] == '?' && S[i + 1 ] == 'o' ) {
S[i] = '.' ;
}
if (i + 1 < N && S[i] == 'o' && S[i + 1 ] == '?' ) {
S[i + 1 ] = '.' ;
}
}
int no = 0 ;
for (char c : S)
if (c == 'o' )
no++ ;
if (no == K) {
rep(i, N) if (S[i] == '?' ) S[i] = '.' ;
cout << S << endl;
return ;
}
auto ps = runLengthEncode(S);
int m = 0 ;
for (auto [c, num] : ps) {
if (c == 'o' )
m += num;
if (c == '?' )
m += (num + 1 ) / 2 ;
}
if (m > K) {
cout << S << endl;
return ;
}
for (auto [c, num] : ps) {
if (c != '?' ) {
rep(i, num) cout << c;
continue ;
}
if (num % 2 == 0 ) {
rep(i, num) cout << '?' ;
} else {
rep(i, num) {
cout << (i % 2 == 0 ? 'o' : '.' );
}
}
}
cout << endl;
}
E - Reachable Set 解説 AC
Fri, Apr 11, 2025 https://atcoder.jp/contests/abc297
A. Double Click https://atcoder.jp/contests/abc297/tasks/abc297_a
B. chess960 https://atcoder.jp/contests/abc297/tasks/abc297_b
C. PC on the Table https://atcoder.jp/contests/abc297/tasks/abc297_c
D. Count Subtractions https://atcoder.jp/contests/abc297/tasks/abc297_d
E. Kth Takoyaki Set https://atcoder.jp/contests/abc297/tasks/abc297_e
ダイクストラみたいな感じで解く。距離 0 のところから始めてコスト $A_i$ で別のノードに移動。距離最初のノードからまたコスト $A_i$ で移動・・・というのを繰り返す。訪れたノードの数が $K+1$ になったら終了(最初の 0 のノードを数えているので $+1$ している)。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, K;
cin >> N >> K;
vll A(N);
rep(i, N) cin >> A[i];
set< ll> check, stock;
stock.insert(0 );
while ((int )check.size() != K + 1 ) {
auto it = stock.begin();
ll x = * it;
stock.erase(it);
check.insert(x);
for (ll a : A)
stock.insert(x + a);
}
cout << * check.rbegin() << endl;
}
F. Minimum Bounding Box 2 https://atcoder.jp/contests/abc297/tasks/abc297_f
Tue, Apr 8, 2025 https://atcoder.jp/contests/abc324
A. Same https://atcoder.jp/contests/abc324/tasks/abc324_a
B. 3-smooth Numbers https://atcoder.jp/contests/abc324/tasks/abc324_b
C. Error Correction https://atcoder.jp/contests/abc324/tasks/abc324_c
D. Square Permutation https://atcoder.jp/contests/abc324/tasks/abc324_d
E. Joint Two Strings https://atcoder.jp/contests/abc324/tasks/abc324_e
$S_i$ の部分列と $T$ の prefix との共通部分の長さが $k$ となる $i$ の個数を $h_k$ とする。
同様に $S_i$ の部分列と $T$ の suffix との共通部分の長さが $k$ となる $i$ の個数を $t_k$ とする。
$T$ の prefix との共通部分の長さが $k$ となる文字には、$T$ の suffix との共通部分の長さが $N-k$ 以上となる文字を連結させれば $T$ を部分列として含むことができる。
よって求める個数は
\begin{align*}
\sum_{k=0}^{N} \left\{ h_k \cdot \left( \sum_{j = N-k}^N t_{j} \right) \right\}
\end{align*}
Tue, Apr 8, 2025 https://atcoder.jp/contests/abc305
A. Water Station https://atcoder.jp/contests/abc305/tasks/abc305_a
B. ABCDEFG https://atcoder.jp/contests/abc305/tasks/abc305_b
C. Snuke the Cookie Picker https://atcoder.jp/contests/abc305/tasks/abc305_c
D. Sleep Log https://atcoder.jp/contests/abc305/tasks/abc305_d
E. Art Gallery on Graph https://atcoder.jp/contests/abc305/tasks/abc305_e
頂点 $i$ に体力 $h_i$ の警備員がいるとき、隣接する頂点に警備員が移動して体力 $h_i - 1$ の警備員がいるとみなしても良い。
体力が大きい警備員がいる頂点から順に隣接する頂点に移動させて、各頂点に体力が 0 以上の警備員がいる頂点が列挙すべき頂点
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, M, K;
cin >> N >> M >> K;
vvint graph(N);
rep(i, M) {
int u, v;
cin >> u >> v;
u-- , v-- ;
graph[u].push_back(v);
graph[v].push_back(u);
}
vll powers(N, - 1 );
rep(i, K) {
int p, h;
cin >> p >> h;
p-- ;
powers[p] = h;
}
// power, node id
using P = pair< ll, int > ;
priority_queue< P> pq;
rep(i, N) {
if (powers[i] > 0 )
pq.push({powers[i], i});
}
while (pq.size()) {
auto [power, id] = pq.top();
pq.pop();
if (powers[id] > power)
continue ;
for (int nx : graph[id]) {
if (powers[nx] >= power - 1 )
continue ;
powers[nx] = power - 1 ;
pq.push({powers[nx], nx});
}
}
vint ans;
rep(i, N) {
if (powers[i] >= 0 )
ans.push_back(i + 1 );
}
cout << ans.size() << endl;
print(ans);
}
F. Dungeon Explore https://atcoder.jp/contests/abc305/tasks/abc305_f
Mon, Apr 7, 2025 https://atcoder.jp/contests/past15-open
E - 合計得点 bit 全探索で良いが $N$ 個から $K$ 個選ぶ方法でも解ける
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n, k;
cin >> n >> k;
vll a(n);
rep(i, n) cin >> a[i];
vint v;
auto dfs = [& ](auto dfs, int used) -> void {
if (__builtin_popcount(used) == k) {
v.push_back(used);
return ;
}
int id = - 1 ;
rep(i, n) {
if ((used >> i) & 1 )
id = i;
}
rep2(i, id + 1 , n) {
dfs(dfs, used | (1 << i));
}
};
dfs(dfs, 0 );
ll ans = 0 ;
for (int used : v) {
rep(i, n) {
if ((used >> i) & 1 )
ans += a[i];
}
}
cout << ans << endl;
}
F - 番号付け void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vint A(N);
rep(i, N) cin >> A[i];
map< int , vint> mp;
rep(i, N) {
mp[A[i]].push_back(i);
}
int cnt = 1 ;
vint ans(N);
for (auto it = mp.begin(); it != mp.end(); it++ ) {
auto [_, ids] = * it;
for (int id : ids) {
ans[id] = cnt++ ;
}
}
print(ans);
}
G - N-SAT void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N, M;
cin >> N >> M;
vvint as(M), bs(M);
rep(i, M) {
int k;
cin >> k;
rep(j, k) {
int a, b;
cin >> a >> b;
a-- ;
as[i].push_back(a);
bs[i].push_back(b);
}
}
rep(t, 1 << N) {
vint xs;
rep(i, N) {
xs.push_back((t >> i) & 1 );
}
int cnt = 0 ;
rep(i, M) {
int ok = 0 ;
int ki = as[i].size();
rep(j, ki) {
if (xs[as[i][j]] == bs[i][j])
ok = 1 ;
}
if (ok)
cnt++ ;
}
if (cnt == M) {
yesno(true);
return ;
}
}
yesno(false);
}
H - 和で表現 解説 AC。愚直解で AC 取れてしまったが解説読んだら二分探索だった。
Sat, Apr 5, 2025 https://atcoder.jp/contests/abc400
C. 2^a b^2 https://atcoder.jp/contests/abc400/tasks/abc400_c
AC したがなぜ AC したのかよくわからず AC した。sqrt が誤差を生むので出てきた数の周辺で検算をするようにして AC したが知識がないとsqrt を使ったときに落とせるテストケースもかけないのでかなり難しい問題に感じた。
$2^a$ を動かして取りうる $b^2$ の個数を求める方法だと $X = 16 = 2^2 \times 2^2 = 2^4 \times 1^2$ のように同じ数に対して重複してカウントしてしまうことがある。
2の冪はすべて $2^a$ の方に押し込んで、$b$ は奇数という制約をかけると重複しない。
\begin{align*}
2^k \times b^2 \leq N
&\Rightarrow b^2 \leq N / 2^k \\
&\Rightarrow b \leq \sqrt{N/2^k} \\
&\Rightarrow b \leq \lfloor \sqrt{N/2^k} \rfloor ~~~(\because b \text{ is an integer})
\end{align*}
Sun, Mar 30, 2025 https://atcoder.jp/contests/past19-open
C - 良さそうな数 / Goodish or Not DP で解いたが、解説読んで普通に桁を変えるのを全探索すればいいだけだった
DP で解く場合は dp[i][j] を左から $i$ 桁目を $j$ にしたときのそれまで変更回数の最小値とする。
// DP 解放
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string S;
cin >> S;
int n = S.size();
if (n == 1 ) {
yesno(true);
return ;
}
vint v(n);
rep(i, n) {
v[i] = S[i] - '0' ;
}
vvint dp(n + 1 , vint(10 , INF));
rep2(i, 1 , 10 ) {
if (v[0 ] != i)
dp[0 ][i] = 1 ;
else
dp[0 ][i] = 0 ;
}
rep2(i, 1 , n) {
rep(j, 10 ) {
int change = v[i] != j;
if (j - 1 >= 0 ) {
chmin(dp[i][j], dp[i - 1 ][j - 1 ] + change);
}
if (j + 1 <= 9 ) {
chmin(dp[i][j], dp[i - 1 ][j + 1 ] + change);
}
chmin(dp[i][j], dp[i - 1 ][j] + change);
}
}
int ok = 0 ;
rep(i, 10 ) {
if (dp[n - 1 ][i] <= 1 )
ok = 1 ;
}
yesno(ok);
}
// 全探索解法
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
string S;
cin >> S;
int n = S.size();
vint v(n);
rep(i, n) {
v[i] = S[i] - '0' ;
}
auto check = [](vint& v) -> bool {
bool ok = true;
int n = v.size();
if (n == 1 )
return true;
if (v[0 ] == 0 )
return false;
rep(i, n - 1 ) {
if (abs(v[i] - v[i + 1 ]) > 1 )
ok = false;
}
return ok;
};
rep(i, n) {
vint t = v;
rep(j, 10 ) {
t[i] = j;
if (check(t)) {
yesno(true);
return ;
}
}
}
yesno(false);
}
K - 隣接禁止 木 DP の問題
Sun, Mar 30, 2025 https://atcoder.jp/contests/abc064
A. i i’s https://atcoder.jp/contests/agc064/tasks/agc064_a
2025/3/30
解説読んでもどうやったらその思考になるのかわからず。
結局諦めた
2025/5/10 リベンジして AC
$N$, $N-1$ を交互に以下の様にまずは並べる.
$$N, N-1, N, \cdots, N-1, N$$次に $N-2$ を両端と、残りの $N-4$ 個を左から条件を満たす部分に挿入していく。
数字を decrement しつつ操作を続け、最後に $2$ は両端、1 は左端か右端のどちらかにおけば条件を満たす数列を構成できる。
$N \leq 1000$ のため愚直に $O(N^2)$ のシミュレーションをしても実行時間制限に間に合う。
より直感的に説明すると $N, N-1$ となっているところに $N-2$ を挿入して $N, N-2, N-1$ となっても $N-2, N-1$ という並びができるおかげで次の $N-3$ を挿入できる場所ができるから、数字を挿入することによって次の数字を挿入できる場所の数は減らない。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
cin >> N;
vint ans(N * 2 - 1 , N);
for (int i = 1 ; i < N * 2 - 1 ; i += 2 ) {
ans[i] = N - 1 ;
}
for (int i = N - 2 ; i >= 1 ; i-- ) {
vint tmp;
int cnt = i;
int m = ans.size();
tmp.push_back(i);
cnt-- ;
rep(j, m) {
tmp.push_back(ans[j]);
if (cnt > 1 && j + 1 < m && tmp.back() != i && ans[j + 1 ] != i && abs(tmp.back() - i) <= 2 && abs(ans[j + 1 ] - i) <= 2 ) {
tmp.push_back(i);
cnt-- ;
}
}
if (cnt)
tmp.push_back(i);
swap(tmp, ans);
}
print(ans);
}
B. Red and Blue Spanning Tree https://atcoder.jp/contests/agc064/tasks/agc064_b
Sun, Mar 30, 2025 https://atcoder.jp/contests/abc399
A. Hamming Distance https://atcoder.jp/contests/abc399/tasks/abc399_a
B. Ranking with Ties https://atcoder.jp/contests/abc399/tasks/abc399_b
C. Make it Forest https://atcoder.jp/contests/abc399/tasks/abc399_c
D. Switch Seats https://atcoder.jp/contests/abc399/tasks/abc399_d
$A_i = A_j = a, (i < j)$ とする。
(1) $i+1=j$ のとき
$a$ が隣接しているので求める整数対の対象にならない
(2) それ以外のとき
求める整数対の候補となるのは
$A_{i-1} = A_{j-1}$ (baba 型) $A_{i-1} = A_{j+1}$ (baab 型) $A_{i+1} = A_{j-1}$ (abba 型) $A_{i+1} = A_{j+1}$ (abab 型) の4つのケースである。
(2.1) $A_{i+1} = A_{j-1}$ のとき
$i+2 = j$ のとき、同じ数字を参照しているので対象外. ($a b a$ で $b$ を参照しているケース) $i+3 = j$ のとき、同じ数字が隣接しているので対象外. ($a b b a$ で $b$ を参照しているケース) それ以外のとき、$(\min(a,b), \max(a,b))$ を答えに追加する (2.2) それ以外の3ケースのとき
Sat, Mar 29, 2025 https://atcoder.jp/contests/past202004-open
K - 括弧 https://atcoder.jp/contests/past202004-open/tasks/past202004_k
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int N;
string S;
cin >> N >> S;
S = "_" + S;
vll C(N + 1 ), D(N + 1 );
rep(i, N) cin >> C[i + 1 ];
rep(i, N) cin >> D[i + 1 ];
// dp[i][j]: i 文字目まで見たときの、対応が取れていない左カッコの数が j のときの最小コスト
+ 1 , vll(N + 1 , INF));
dp[0 ][0 ] = 0 ;
rep2(i, 1 , N + 1 ) {
rep(j, N) {
if (S[i] == '(' ) {
chmin(dp[i][j + 1 ], dp[i - 1 ][j]);
// 反転
if (j - 1 >= 0 )
chmin(dp[i][j - 1 ], dp[i - 1 ][j] + C[i]);
} else {
if (j - 1 >= 0 )
chmin(dp[i][j - 1 ], dp[i - 1 ][j]);
// 反転
+ 1 ], dp[i - 1 ][j] + C[i]);
}
// i 番目の要素を削除
- 1 ][j] + D[i]);
}
}
cout << dp[N][0 ] << endl;
}
Fri, Mar 28, 2025 A. Repdigit Number https://atcoder.jp/contests/arc149/tasks/arc149_a
自力 AC
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, M;
cin >> N >> M;
modint:: set_mod(M);
using mint = modint;
auto chmin_string = [](string& a, string& b) -> void {
if (a.size() > b.size()) return ;
if (a.size() < b.size()) {
a = b;
return ;
}
if (a < b) a = b;
};
string ans = "" ;
rep2(i, 1 , 10 ) {
string s = "" ;
mint x = 0 ;
rep(j, N) {
x *= 10 ;
x += i;
s.push_back('0' + i);
if (x == 0 ) chmin_string(ans, s);
}
}
if (ans == "" ) ans = "-1" ;
cout << ans << endl;
}
B. Two LIS Sum https://atcoder.jp/contests/arc149/tasks/arc149_b
Fri, Mar 28, 2025 A. Operations on a Stack https://atcoder.jp/contests/arc194/tasks/arc194_a
$d(i,1)$ を $i$ 番目の要素を使うときの総和の最大値、$d(i,0)$ を $i$ 番目の要素を使わないときの総和の最大値とする。
$i$ 番目の要素を使うとき、$i-1$ 番目の要素を使う場合、使わない場合の値いずれかの場合からの遷移がある。
$i$ 番目の要素を使わないとき、$i-1$ 番目の要素を積んで、その後その要素を捨てる操作になるから、$i-2$ 番目の要素を使う場合、使わない場合のうちの大きい方の値を選べばよい。
\begin{align}
d(i,1) &= \max(dp(i-1, 1), dp(i-1, 0)) + A_i \nonumber \\
d(i,0) &= \max(dp(i-2, 1), dp(i-2, 0)) \nonumber
\end{align}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n;
cin >> n;
vll a(n + 1 );
rep(i, n) cin >> a[i + 1 ];
// dp[i][j]: i 回目の操作で操作 j を行ったときの S の総和の最大値
// j = 0: 何もしない
// j = 1: a[i] を入れる
+ 1 , vll(2 , - INF));
dp[0 ][1 ] = 0 ;
rep2(i, 1 , n + 1 ) {
chmax(dp[i][1 ], dp[i - 1 ][1 ] + a[i]);
chmax(dp[i][1 ], dp[i - 1 ][0 ] + a[i]);
if (i - 2 >= 0 ) {
// i-1 回目で要素を入れて、i 回目で要素を取り出すと何もしていないのと同じ
0 ], dp[i - 2 ][1 ]);
chmax(dp[i][0 ], dp[i - 2 ][0 ]);
}
}
cout << max(dp[n][0 ], dp[n][1 ]) << '\n' ;
}
B. Minimum Cost Sort https://atcoder.jp/contests/arc194/tasks/arc194_b
Tue, Mar 25, 2025 https://atcoder.jp/contests/abc244
A. Last Letter https://atcoder.jp/contests/abc244/tasks/abc244_a
B. Go Straight and Turn Right https://atcoder.jp/contests/abc244/tasks/abc244_b
C. Yamanote Line Game https://atcoder.jp/contests/abc244/tasks/abc244_c
D. Swap Hats https://atcoder.jp/contests/abc244/tasks/abc244_d
E. King Bombee https://atcoder.jp/contests/abc244/tasks/abc244_e
dp[k][i][j]: $k$ 回移動後、頂点 $i$ にたどり着くまでに頂点 $X$ を偶数($j=0$)/奇数($j=1$)回訪れる経路の数
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, M, K, S, T, X;
cin >> N >> M >> K >> S >> T >> X;
S-- , T-- , X-- ;
vvint graph(N);
rep(i, M) {
int u, v;
cin >> u >> v;
u-- , v-- ;
graph[u].push_back(v);
graph[v].push_back(u);
}
// dp[k][i][j]: k 回移動後、頂点 i にたどり着くまでに頂点 X を偶数(j=0)/奇数(j=1)回訪れる経路の数
< vector< vector< mint>>> dp(K + 1 , vector< vector< mint>> (N, vector< mint> (2 )));
dp[0 ][S][0 ] = 1 ;
rep2(i, 1 , K + 1 ) {
rep(j, N) {
for (int nx : graph[j]) {
if (nx == X) {
dp[i][nx][0 ] += dp[i - 1 ][j][1 ];
dp[i][nx][1 ] += dp[i - 1 ][j][0 ];
} else {
dp[i][nx][0 ] += dp[i - 1 ][j][0 ];
dp[i][nx][1 ] += dp[i - 1 ][j][1 ];
}
}
}
}
cout << dp[K][T][0 ].val() << endl;
}
F. Shortest Good Path https://atcoder.jp/contests/abc244/tasks/abc244_f
Mon, Mar 24, 2025 https://atcoder.jp/contests/abc286
A. Range Swap https://atcoder.jp/contests/abc286/tasks/abc286_a
B. Cat https://atcoder.jp/contests/abc286/tasks/abc286_b
C. Rotate and Palindrome https://atcoder.jp/contests/abc286/tasks/abc286_c
D. Money in Hand https://atcoder.jp/contests/abc286/tasks/abc286_d
E. Souvenir https://atcoder.jp/contests/abc286/tasks/abc286_e
ワーシャルフロイドで解く。距離が短い場合は価値も更新. 距離が同じ場合は価値を高い方に更新する。
はじめわーシャルフロイドの添字の実行順があったことを忘れて WA したが、なぜか3回回したら AC した。
まぐれと思ったが3回実行すると正しい答えが返ってくることは証明されているらしい。
https://qiita.com/tmaehara/items/f56be31bbb7a468a04ed
コード中の注意点として距離が大きいときの条件と同じときの条件をまとめて書いてはいけない
OK
if (dist[i][j] > dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
value[i][j] = value[i][k] + value[k][j] - prices[k];
}
if (dist[i][j] == dist[i][k] + dist[k][j]) {
chmax(value[i][j], value[i][k] + value[k][j] - prices[k]);
}
NG
if (dist[i][j] >= dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
chmax(value[i][j], value[i][k] + value[k][j] - prices[k]);
}
NG 版で書くと距離が大きいときの価値の値を使ってしまうことがあるため WA する。
Sun, Mar 23, 2025 https://atcoder.jp/contests/abc320
A. Leyland Number https://atcoder.jp/contests/abc320/tasks/abc320_a
B. Longest Palindrome https://atcoder.jp/contests/abc320/tasks/abc320_b
C. Slot Strategy 2 (Easy) https://atcoder.jp/contests/abc320/tasks/abc320_c
D. Relative Position https://atcoder.jp/contests/abc320/tasks/abc320_d
E. Somen Nagashi https://atcoder.jp/contests/abc320/tasks/abc320_e
並んでいる人は id が小さい順で常に並んでいる、列から離れた人は帰ってくる時間が小さい順に並んでいると考えればそれぞれを priority queue で管理すれば問題が解けることがわかる
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n, m;
cin >> n >> m;
vll ans(n);
priority_queue< int , vint, greater< int >> people;
// time, id
using P = pair< ll, int > ;
priority_queue< P, vector< P> , greater< P>> tpq;
rep(i, n) people.push(i);
rep(i, m) {
ll t, w, s;
cin >> t >> w >> s;
// そうめんが流れてくるまでに列に戻ってくる人を列に戻す
while (tpq.size() && tpq.top().first <= t) {
auto [t, id] = tpq.top();
tpq.pop();
people.push(id);
}
// 列に誰もいなかったら何もしない
if (people.size() == 0 )
continue ;
auto p = people.top();
people.pop();
ans[p] += w;
tpq.push({t + s, p});
}
for (ll x : ans)
cout << x << '\n' ;
}
F. Fuel Round Trip https://atcoder.jp/contests/abc320/tasks/abc320_f
Sun, Mar 23, 2025 https://atcoder.jp/contests/abc398
A. Doors in the Center https://atcoder.jp/contests/abc398/tasks/abc398_a
B. Full House 3 https://atcoder.jp/contests/abc398/tasks/abc398_b
C. Uniqueness https://atcoder.jp/contests/abc398/tasks/abc398_c
D. Bonfire https://atcoder.jp/contests/abc398/tasks/abc398_d
煙の位置は変えずに焚き火と高橋くんの位置を移動させる。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll n, row, col;
cin >> n >> row >> col;
string s;
cin >> s;
using P = pair< ll, ll> ;
set< P> memo;
memo.insert({0 , 0 });
int si = 0 , sj = 0 ;
for (char c : s) {
if (c == 'N' ) {
si++ ;
row++ ;
}
if (c == 'W' ) {
sj++ ;
col++ ;
}
if (c == 'S' ) {
si-- ;
row-- ;
}
if (c == 'E' ) {
sj-- ;
col-- ;
}
memo.insert({si, sj});
if (memo.count({row, col})) {
cout << 1 ;
} else {
cout << 0 ;
}
}
cout << endl;
}
E. Tree Game https://atcoder.jp/contests/abc398/tasks/abc398_e
Sat, Mar 22, 2025 A. Exchange https://atcoder.jp/contests/arc177/tasks/arc177_a
B. Puzzle of Lamps https://atcoder.jp/contests/arc177/tasks/arc177_b
C. Routing https://atcoder.jp/contests/arc177/tasks/arc177_c
条件1について考える。赤色のマスを紫色に塗ってもスタートとゴールの連結性は変わらないから紫色に変えるべきマスは青色のマスである。
同様に条件2を達成するためには赤色のマスを紫色に変える必要がある。
よって条件1, 2を満たすために必要な紫色に変えるマスは独立して考えることができる。
よって問題の部分問題は次のように言い換えることができる。
各マスは赤か白で塗られており $c_{i,j} = 'R'$ のとき赤、$c_{i,j} = 'W'$ のとき白で塗られている。赤マス間は自由に行き来することできる。
スタートとゴールは赤マスである。
スタートとゴールが連結なるためには最低何マス追加で赤マスに変える必要があるか。
これを青マスについても同様に解いて、その和を求めればよい。
白マスへの移動はコスト $+1$、それ以外の移動は コスト $0$ であると考えると、スタートからゴールまでの最短経路を求める問題として解くことができる。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n;
cin >> n;
vector< vector< char >> B(n, vector< char > (n, '_' )), R(n, vector< char > (n, '_' ));
rep(i, n) {
rep(j, n) {
char c;
cin >> c;
if (c == 'R' )
R[i][j] = c;
else
B[i][j] = c;
}
}
vint di = {1 , 0 , - 1 , 0 };
vint dj = {0 , - 1 , 0 , 1 };
auto cal = [& ](vector< vector< char >>& grid, int si, int sj, int ti, int tj) -> ll {
vvll dist(n, vll(n, INF));
dist[si][sj] = 0 ;
using P = tuple< int , int , int > ;
priority_queue< P, vector< P> , greater< P>> que;
que.push({0 , si, sj});
while (que.size()) {
auto [cost, i, j] = que.top();
que.pop();
if (dist[i][j] < cost)
continue ;
rep(d, 4 ) {
int ni = i + di[d], nj = j + dj[d];
if (clamp(ni, 0 , n - 1 ) != ni || clamp(nj, 0 , n - 1 ) != nj)
continue ;
if (grid[ni][nj] == '_' ) {
if (dist[ni][nj] <= dist[i][j] + 1 )
continue ;
dist[ni][nj] = dist[i][j] + 1 ;
} else {
if (dist[ni][nj] <= dist[i][j])
continue ;
dist[ni][nj] = dist[i][j];
}
que.push({dist[ni][nj], ni, nj});
}
}
return dist[ti][tj];
};
ll ans = cal(R, 0 , 0 , n - 1 , n - 1 ) + cal(B, 0 , n - 1 , n - 1 , 0 );
cout << ans << endl;
}
D. Earthquakes https://atcoder.jp/contests/arc177/tasks/arc177_d
Sat, Mar 22, 2025 A. Chmax Rush https://atcoder.jp/contests/arc182/tasks/arc182_a
解説 AC
$i$ 番目の操作は、左操作か、右操作か、どちらでも良いかの3通りがある。
$i$ 番目の操作が左か右操作のいずれかに確定している場合はそれを実行しなければならないので、$2^\text{どちらの操作をしても良い回数}$ が答えとなる
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n, q;
cin >> n >> q;
vint P(q), V(q);
rep(i, q) {
cin >> P[i] >> V[i];
P[i]-- ;
}
// kind[i]: i 回目にどの操作を必要があるか
// -1 左操作
// 1 右操作
// 0 どちらでも良い
auto change = [& ](int i, int op) -> bool {
if (kind[i] == 0 ) {
kind[i] = op;
return true;
}
if (kind[i] != op) {
// 操作が矛盾
return false;
}
return true;
};
rep(i, q) {
rep2(j, i + 1 , q) {
if (V[i] <= V[j])
continue ;
if (P[i] == P[j]) {
cout << 0 << endl;
return ;
}
bool ok = true;
if (P[i] < P[j]) {
// i 番目の操作で左操作
// j 番目の操作で右操作
// をしなければならない
= ok && change(i, - 1 );
ok = ok && change(j, 1 );
}
if (P[i] > P[j]) {
// i 番目の操作で右操作
// j 番目の操作で左操作
// をしなければならない
= ok && change(i, 1 );
ok = ok && change(j, - 1 );
}
if (! ok) {
cout << 0 << endl;
return ;
}
}
}
mint two = 2 ;
ll cnt = 0 ;
rep(i, q) cnt += kind[i] == 0 ;
cout << two.pow(cnt).val() << endl;
}
B. |{floor(A_i/2^k)}| https://atcoder.jp/contests/arc182/tasks/arc182_b
Fri, Mar 21, 2025 https://atcoder.jp/contests/abc322
A. First ABC 2 https://atcoder.jp/contests/abc322/tasks/abc322_a
B. Prefix and Suffix https://atcoder.jp/contests/abc322/tasks/abc322_b
C. Festival https://atcoder.jp/contests/abc322/tasks/abc322_c
D. Polyomino https://atcoder.jp/contests/abc322/tasks/abc322_d
E. Product Development https://atcoder.jp/contests/abc322/tasks/abc322_e
解説 AC.
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n, k, p;
cin >> n >> k >> p;
vll c(n + 1 );
vvll A(n + 1 , vll(k));
rep(i, n) {
cin >> c[i + 1 ];
rep(j, k) {
cin >> A[i + 1 ][j];
}
}
vector< map< vll, ll>> dp(n + 1 );
dp[0 ][vll(k, 0 )] = 0 ;
rep2(i, 1 , n + 1 ) {
dp[i] = dp[i - 1 ];
for (auto [v, val] : dp[i - 1 ]) {
vll t = v;
rep(j, k) {
t[j] += A[i][j];
if (t[j] > p)
t[j] = p;
}
if (dp[i].count(t)) {
chmin(dp[i][t], val + c[i]);
} else {
dp[i][t] = val + c[i];
}
}
}
vll v(k, p);
if (dp[n].count(v)) {
cout << dp[n][v] << endl;
} else {
cout << - 1 << endl;
}
}
F. Vacation Query https://atcoder.jp/contests/abc322/tasks/abc322_f
Thu, Mar 20, 2025 https://atcoder.jp/contests/abc303
A. Similar String https://atcoder.jp/contests/abc303/tasks/abc303_a
B. Discord https://atcoder.jp/contests/abc303/tasks/abc303_b
C. Dash https://atcoder.jp/contests/abc303/tasks/abc303_c
D. Shift vs. CapsLock https://atcoder.jp/contests/abc303/tasks/abc303_d
E. A Gift From the Stars https://atcoder.jp/contests/abc303/tasks/abc303_e
葉から始めて距離が3離れたノードは別の star graph の葉に相当する。また葉の隣のノードは star graph の中心。
これよりある葉から出発して $3i+1$ 離れたノードは star graph の中心だったものである。
これより中心の頂点番号が取れるのでそのノードにおける次数を昇順に出力すればよい。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n;
cin >> n;
vvint graph(n);
rep(i, n - 1 ) {
int u, v;
cin >> u >> v;
u-- , v-- ;
graph[u].push_back(v);
graph[v].push_back(u);
}
vint sz;
auto dfs = [& ](auto dfs, int now, int p, int label) -> void {
if (label == 1 ) {
sz.push_back(graph[now].size());
}
for (int nx : graph[now]) {
if (nx == p)
continue ;
dfs(dfs, nx, now, (label + 1 ) % 3 );
}
};
rep(i, n) if (graph[i].size() == 1 ) {
dfs(dfs, i, - 1 , 0 );
break ;
}
sort(all(sz));
print(sz);
}
F. Damage over Time https://atcoder.jp/contests/abc303/tasks/abc303_f
Thu, Mar 20, 2025 A. Right String https://atcoder.jp/contests/arc140/tasks/arc140_a
解説 AC。
答えが $N$ の約数のいずれかになることまではわかったが最終的な答えの求め方を間違えた。
$d|N$ となる $d$ について考える。$S$ を下記のように $d$ 個ずつに分割する。
1 2 $\cdots$ d $S_1$ $S_2$ $\cdots$ $S_d$ $S_{d+1}$ $S_{d+2}$ $\cdots$ $S_{2d}$ $\vdots$ $\vdots$ $\ddots$ $\vdots$ $S_{N-d+1}$ $S_{N-d+2}$ $\cdots$ $S_N$
列 $i$ に対して最頻出文字に全ての文字を置き換えるのに必要な操作回数を $c_i$ とすると $\sum_i c_i \leq K$ のとき題意の操作を実行してできる文字種は $d$ になる。よって $f(S) \leq d$.
同様に全ての $N$ の約数について調べ $f(S) \leq d$ を達成できる最小の $d$ が答え。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n, k;
string s;
cin >> n >> k >> s;
ll ans = n;
rep2(d, 1 , n) {
if (n % d)
continue ;
int sum = 0 ;
rep(i, d) {
vint cnt(26 , 0 );
for (int j = i; j < n; j += d) {
cnt[s[j] - 'a' ]++ ;
}
sum += * max_element(all(cnt));
}
if (n - sum <= k)
chmin(ans, d);
}
cout << ans << endl;
}
Mon, Mar 17, 2025 https://atcoder.jp/contests/abctypical90
001. Yokan Party(★4) https://atcoder.jp/contests/typical90/tasks/typical90_a
解説 AC
最小値を最大化する問題は二分探索を使うのが定石らしい。
最小値を $m$ としたときの分割数が $K+1$ 以上ならば最小値を $m$ 以上にすることができる。そうでないならば最小値を $m$ にすることはできない。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, L, K;
cin >> N >> L >> K;
vll A(N);
rep(i, N) cin >> A[i];
A.insert(A.begin(), 0 );
A.push_back(L);
vll diff;
rep(i, N + 1 ) {
diff.push_back(A[i + 1 ] - A[i]);
}
int m = diff.size();
ll ac = 0 , wa = L + 1 ;
while (abs(ac - wa) > 1 ) {
ll wj = (ac + wa) / 2 ;
int i = 0 ;
ll cnt = 0 ;
ll sum = 0 ;
rep(i, m) {
sum += diff[i];
if (sum >= wj) {
sum = 0 ;
cnt++ ;
}
}
if (cnt >= K + 1 ) {
ac = wj;
} else {
wa = wj;
}
}
cout << ac << endl;
}
002 - Encyclopedia of Parentheses(★3) https://atcoder.jp/contests/typical90/tasks/typical90_b
Sun, Mar 16, 2025 A. Neq Number https://atcoder.jp/contests/arc173/tasks/arc173_a
$x$ 以下の Neq Number の個数を求める関数を書いて二分探索すれば良いという方針は立ったが実装に手間取った。
結局うまく実装できず解説を読んだり解説放送を見たが詳細な実装方法については触れておらず結局自分で考えた。
$f(x)$ を $x$ 以下の Neq Number の個数とする。$f(x) = K$ となる最小の $x$ が求める答えとなる。
$f(x)$ は広義単調増加関数であるから二分探索で答えを求めることができる。
$d$ 桁の Neq Number の個数を考える。左の桁を 0 桁目とすると 0 桁目は 1 から 9 までの 9 通りである。
$i > 0$ 桁目の数は 0~9 の10通りのうち $i-1$ 桁目とは異なる数であるであるから 9 通りである。
よって $d$ 桁の Neq Number の個数は $9^{d}$ 通りである。
$f(x)$ の実装について考える。
$x$ が1桁のとき $f(x) = x$ である。
$x$ が $d$ 桁のとき まず $d$ 桁未満の Neq Number の個数は $\sum_{k=1}^{d-1} 9^{k}$ である。
Sun, Mar 16, 2025 https://atcoder.jp/contests/abc397
A. Thermometer https://atcoder.jp/contests/abc397/tasks/abc397_a
B. Ticket Gate Log https://atcoder.jp/contests/abc397/tasks/abc397_b
C. Variety Split Easy https://atcoder.jp/contests/abc397/tasks/abc397_c
D. Cubes https://atcoder.jp/contests/abc397/tasks/abc397_d
解説 AC
$d = x-y$ とすると
\begin{align*}
x^3 - y^3
&= (d+y)^3 - y^3 \\
&= d^3 + 3d^2y + 3dy^2 + y^3 - y^3 \\
&= d^3 + 3d^2y + 3dy^2 \\
&= N
\end{align*}
となる。ここで $3d^2y + 3dy^2 > 0$ だから $d^3 < N$ である。
さらに
\begin{align*}
&x^3 - y^3 = N \\
&(x-y)(x^2 + xy + y^2) = N \\
&d((d+y)^2 + (d+y)y + y^2) = N \\
&(d^2 + 2dy + y^2) + (dy + y^2) + y^2 = N/d \\
&3y^2 + 3dy + d^2 - N/d = 0
\end{align*}
Sun, Mar 16, 2025 https://atcoder.jp/contests/abc216
E - Amusement Park https://atcoder.jp/contests/abc216/tasks/abc216_e
貪欲解法 明らかに、楽しさが大きいアトラクションから乗るのが最適である。
愚直に priority queue などに数値を入れてシミュレーションをすると時間がかかりすぎて TLE になる。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll n, k;
cin >> n >> k;
vll a(n);
rep(i, n) cin >> a[i];
map< ll, ll> mp;
for (ll x : a)
mp[x]++ ;
ll ans = 0 ;
while (mp.rbegin() != mp.rend() && k) {
auto it = mp.rbegin();
auto nit = next(it);
ll v1 = it-> first;
ll n1 = it-> second;
ll v2 = 0 ;
if (nit != mp.rend())
v2 = nit-> first;
if ((v1 - v2) * n1 <= k) {
k -= (v1 - v2) * n1;
ans += cal(v2, v1) * n1;
mp.erase(v1);
if (v2)
mp[v2] += n1;
} else {
ll q = k / n1;
ll r = k % n1;
ans += cal(v1 - q, v1) * n1;
v1 -= q;
ans += v1 * r;
k = 0 ;
}
}
cout << ans << endl;
}
二分探索解法 楽しさが 0 以下のアトラクションに乗る意味はないから楽しさが 0 より大きい場合を考える。
問題は楽しさが $1, 2, \cdots, A_1, 1, 2, \cdots, A_2, \cdots, 1,2, \cdots, A_N$ である $\sum_i A_i$ 個のアトラクションから $K$ 個選んで乗ったときの楽しさの総和の最大値を求める問題と読み替えることができる。
Fri, Mar 14, 2025 D - aab aba baa https://atcoder.jp/contests/abc202/tasks/abc202_d
はじめの文字が a となる場合の数は $A-1$ 個の a と $B$ 個の b の並び替え方の場合の数だから $\frac{(A+B+1)!}{(A-1)!B!}$ である。
よって $K > \frac{(A+B+1)!}{(A-1)!B!}$ のときは b から始まる。
この性質を使って先頭から文字を決めていく。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll a, b, k;
cin >> a >> b >> k;
int m = a + b;
vvll dp(m + 1 , vll(m + 1 , 0 ));
dp[0 ][0 ] = 1 ;
rep(i, m + 1 ) {
rep(j, m + 1 ) {
if (i > 0 )
dp[i][j] += dp[i - 1 ][j];
if (j > 0 )
dp[i][j] += dp[i][j - 1 ];
}
}
string ans = "" ;
auto dfs = [& ](auto dfs, ll na, ll nb, ll rem) {
if (na == 0 && nb == 0 ) {
return ;
}
if (na == 0 ) {
ans.push_back('b' );
dfs(dfs, na, nb - 1 , rem);
return ;
}
if (nb == 0 ) {
ans.push_back('a' );
dfs(dfs, na - 1 , nb, rem);
return ;
}
ll v = dp[na - 1 ][nb];
if (rem <= v) {
ans.push_back('a' );
dfs(dfs, na - 1 , nb, rem);
return ;
}
ans.push_back('b' );
dfs(dfs, na, nb - 1 , rem - v);
};
dfs(dfs, a, b, k);
cout << ans << endl;
}
Thu, Mar 13, 2025 D - Journey https://atcoder.jp/contests/abc194/tasks/abc194_d
クーポンコレクター問題
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n;
cin >> n;
double ans = 0 ;
rep2(i, 1 , n) {
ans += 1.0 / i;
}
printf("%.9lf \n " , ans * n);
}
Tue, Mar 11, 2025 A. Union of Grid Paths https://atcoder.jp/contests/arc197/tasks/arc197_a
条件より $X$ は左上から右下への経路になる。考えうる経路で1度でも通るマスの数を求める問題。
到達するマスの下限となる経路は ? において D が選択できるならば選択し、そうでなければ R を選択した経路である。
上限となる経路は ? において R が選択できるならば選択し、そうでなければ D を選択した経路である。
左上から 1 step ずつ上限・下限の経路で進めていたときの座標をそれぞれ $(h_u, w_u)$, $(h_l, w_l)$ とすると $h_l - h_u = w_u - w_l$ となっている。
$d = h_l - h_u$ とすると、途中の ? の選択の仕方で $(h_l, w_l), (h_{l}-1, w_{l}+1), \cdots, (h_{l}-d, w_{l}+d) = (h_u, w_u)$ の $d+1$ 個のマスを黒く塗ることができる。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
auto cal = []() -> void {
int H, W;
string S;
cin >> H >> W >> S;
int ld = 0 , rr = 0 ;
for (char c : S) {
if (c == 'D' )
ld++ ;
if (c == 'R' )
rr++ ;
}
ll ans = 1 ;
int l = 0 , r = 0 ;
for (char c : S) {
if (c == 'D' ) {
l++ ;
r++ ;
}
if (c == '?' ) {
if (ld < H - 1 ) {
ld++ ;
l++ ;
}
if (rr < W - 1 ) {
rr++ ;
} else {
r++ ;
}
}
ans += l - r + 1 ;
}
cout << ans << endl;
};
int t;
cin >> t;
rep(i, t) {
cal();
}
}
B. Greater Than Average https://atcoder.jp/contests/arc197/tasks/arc197_b
Mon, Mar 10, 2025 E - Our clients, please wait a moment https://atcoder.jp/contests/abc325/tasks/abc325_e
類題: https://atcoder.jp/contests/abc395/tasks/abc395_e
社用車だけを使ったときの場合のグラフ $G$ と電車だけを使った場合のグラフ $G^\prime$ を作り、$G$ の各ノードから同じ都市に対応する $G^\prime$ のノードへコスト 0 の辺を張る。
都市 $i$ に対応する $G$ におけるノード番号を $i$, $G^\prime$ におけるノードの番号を $N + i$ とする。
求める答えはノード 1 から出発してノード $N$ またはノード $2N$ に到達するまでの最小コストである。
($1 \rightarrow N+1$ への移動はコスト 0 でできるから出発は 1 から出発するケースだけ考えればよい)
struct Edge {
ll to, cost;
};
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n, a, b, c;
cin >> n >> a >> b >> c;
vvll D(n, vll(n));
rep(i, n) rep(j, n) cin >> D[i][j];
vector< vector< Edge>> graph(n * 2 );
rep(i, n) rep(j, n) {
if (i == j)
continue ;
graph[i].push_back({j, D[i][j] * a});
graph[j].push_back({i, D[i][j] * a});
graph[n + i].push_back({n + j, D[i][j] * b + c});
graph[n + j].push_back({n + i, D[i][j] * b + c});
}
rep(i, n) graph[i].push_back({n + i, 0 });
vll dist(n * 2 , INF);
dist[0 ] = 0 ;
// cost, pos
using P = pair< ll, ll> ;
priority_queue< P, vector< P> , greater< P>> pq;
pq.push({0 , 0 });
while (pq.size()) {
auto [cost, now] = pq.top();
pq.pop();
if (dist[now] < cost)
continue ;
for (auto [to, cost] : graph[now]) {
if (dist[to] <= dist[now] + cost)
continue ;
dist[to] = dist[now] + cost;
pq.push({dist[to], to});
}
}
cout << min(dist[n - 1 ], dist[n * 2 - 1 ]) << '\n' ;
}
Sun, Mar 9, 2025 はじめに 木マスター養成講座 で普通のセグメント木ををソラでかけるようになったあとに、「遅延評価セグメント木をソラで書きたいあなたに 」 (以降ソラ版と呼ぶ)を読んで遅延評価セグメント木をソラでかけるようになった。
とはいえ、ソラで書くの面倒なので ACL に移行するために「AtCoder LibraryのLazy Segtreeの使い方 」を読んでみたものの、lazy 配列の使い方がソラ版と違っていて対応関係がよくわからなかったのでまとめる。
主な違いまとめ ソラ版は lazy node に入れた値を自分の data node に適用するが、ACL 版だと子の data node に適用している ソラ版は lazy node に配列が被覆している範囲分も含めて値が入っているが、ACL 版だと範囲分は含まれていない例区間加算で範囲に $x$ を加算する場合を考える ソラ版は範囲の長さが $n$ なら lazy node に $n \times x$ が入っているが、ACL 版だと $x$ が入っている ACL 版の場合は長さの情報は data node にもたせて lazy node のデータを data node に適用するときに使う ソラ版の eval 関数は ACL 版の mapping 関数と composition 関数を同時にやっているようなもの ACL 版を使うときの S, op, e, F, mapping, composition はそれぞれ何を表しているのか
Sun, Mar 9, 2025 C - Buy Balls https://atcoder.jp/contests/abc396/tasks/abc396_c
嘘解法で解いてしまった。配列の範囲外参照していたが AC してしまった。
黒・白ともに降順にソートしておく。
値が正の黒ボールをまず全て取る。その時の数を $N_b$ とする。
次に $N_b$ 個を超えないように正の値の白ボールを取る。その時の数を $N_w$ とする。
$N_w < N_b$ のときは、追加で白ボールをとっても価値は増えないのでこれ以上取る意味はない。
$N_w = N_b$ のときを考える。
このとき、白ボールを取得すると黒ボールの個数を超えてしまうため、黒ボールも同時に取得する必要がある。
よって、追加で白ボールを取ったほうが良い状況は、$B_{N_b+1} + W_{N_w+1} > 0$ が成り立つときである。
これをボールがなくなるか、条件を満たさなくなるまで繰り返す。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
int n, m;
cin >> n >> m;
vll b(n), w(m);
rep(i, n) cin >> b[i];
rep(i, m) cin >> w[i];
sort(rall(b));
sort(rall(w));
ll ans = 0 ;
int nb = 0 ;
rep(i, n) {
if (b[i] >= 0 ) {
ans += b[i];
nb++ ;
}
}
int nw = 0 ;
while (nw < m && nb > nw && w[nw] > 0 ) { // コンテスト中のコードだと nw < m を入れ忘れた
+= w[nw];
nw++ ;
}
while (nw < m && nb < n && w[nw] + b[nb] >= 0 ) {
ans += w[nw] + b[nb];
nw++ ;
nb++ ;
}
cout << ans << endl;
}
解説の想定解法
Sat, Mar 8, 2025 E - Mancala 2 https://atcoder.jp/contests/abc340/tasks/abc340_e
区間加算、一点取得の問題。ac-library を使うと lazy segment tree が必要になってセットアップが大変だが自分でセグメントツリーを実装すると意外と簡単。
かつっぱ氏の木マスター養成講座がわかりやすい
ref: https://youtu.be/g30mEb4jE2g?si=g-oLairJqPWzWHn6
struct SegmentTree {
vll seg;
int len;
SegmentTree(int n) {
rep(i, 30 ) {
if (n <= (1 << i)) {
len = 1 << i;
break ;
}
}
seg.resize(len * 2 , 0 );
}
ll get (int p) {
p += len;
ll ans = seg[p];
while (p / 2 ) {
p /= 2 ;
ans += seg[p];
}
return ans;
}
void add (int l, int r, ll x) {
l += len, r += len;
while (l < r) {
if (l & 1 ) {
seg[l] += x;
l++ ;
}
l /= 2 ;
if (r & 1 ) {
seg[r - 1 ] += x;
r-- ;
}
r /= 2 ;
}
}
};
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll n, m;
cin >> n >> m;
SegmentTree seg(n);
rep(i, n) {
ll a;
cin >> a;
seg.add(i, i + 1 , a);
}
rep(i, m) {
int b;
cin >> b;
ll x = seg.get(b);
seg.add(b, b + 1 , - x);
b++ ;
ll q = x / n;
ll r = x % n;
seg.add(0 , n, q);
if (b + r >= n) {
seg.add(b, n, 1 );
seg.add(0 , b + r - n, 1 );
} else {
seg.add(b, b + r, 1 );
}
}
rep(i, n) {
if (i != 0 )
cout << ' ' ;
cout << seg.get(i);
}
cout << endl;
}
Thu, Mar 6, 2025 E - Modulo MST $N = 8$ のときの完全グラフのときの辺の数は $\displaystyle \frac{N(N-1)}{2} = \frac{8 \times 7}{2} = 28$ でここから $N-1=7$ ほんの辺を選ぶ選び方は $_{28}\mathrm{C}_7 = 1,184,040$ 通りなので全探索が間に合う。
各頂点について自身を含めて他のどの頂点に辺を張るかということを考える場合でも $N^{N-1} = 8^7 = 2,097,152$ こっちの方法でも間に合う。
$N-1$ 本の辺を張る実装
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll n, m, k;
cin >> n >> m >> k;
vector< tuple< ll, ll, ll>> es;
rep(i, m) {
ll u, v, w;
cin >> u >> v >> w;
u-- , v-- ;
es.emplace_back(u, v, w);
}
ll ans = INF;
auto dfs = [& ](auto dfs, int depth, vint used) {
if (used.size() == n - 1 ) {
dsu uf(n);
ll sum = 0 ;
for (int i : used) {
auto [u, v, w] = es[i];
if (uf.same(u, v))
return ;
uf.merge(u, v);
sum += w;
sum %= k;
}
chmin(ans, sum);
return ;
}
if (depth == m) {
return ;
}
dfs(dfs, depth + 1 , used);
used.push_back(depth);
dfs(dfs, depth + 1 , used);
};
dfs(dfs, 0 , {});
cout << ans << endl;
}
辺が存在するかわからないがとりあえず考えうるパターンを確認する実装
Wed, Mar 5, 2025 D - Diagonal Separation https://atcoder.jp/contests/abc386/tasks/abc386_d
解説 AC
黒マスの座標を $(x,y)$ とすると $(i,j) \in [1,x] \times [1,y]$ のマスに白マスが存在しないことが条件である。
与えられたマスを辞書順に sort して上記の条件と合致するか確認する。
頭から順に確認していき
白マスならばそれまで出た白マスの中で最小の $y$ 座標を記録する 黒マスならばそれまで出た白マスの中で最小の $y$ 座標より大きいか確認する とすればよい。
void solve () {
int n, m;
cin >> n >> m;
vector< tuple< int , int , char >> qs;
rep(i, m) {
int x, y;
char c;
cin >> x >> y >> c;
qs.emplace_back(x, y, c);
}
sort(all(qs));
int cnum = INF;
for (auto [x, y, c] : qs) {
if (c == 'B' ) {
if (cnum <= y) {
yesno(false);
return ;
}
} else {
chmin(cnum, y);
}
}
yesno(true);
}
E - Maximize XOR https://atcoder.jp/contests/abc386/tasks/abc386_e
Sat, Mar 1, 2025 D - Pigeon Swap https://atcoder.jp/contests/abc395/tasks/abc395_d
想定と違う方法で解けたがすごく複雑なことをしてしまった。
提出コードでは鳩 $i$ が配置されたときの index とその時の巣の番号と、箱を swap したときの履歴を管理して解いた。
種別 1 のクエリで鳩を移動させたあとに箱の swap があった場合は、swap の履歴をたどって最終的な巣の番号を求めた。
void solve () {
int N, Q;
cin >> N >> Q;
// 配置されたときの index, その時の巣の番号
< pair< int , int >> hato(N);
// 入れ替えがあったときの index, 移動先の巣の番号
< vector< pair< int , int >>> hako(N);
rep(i, N) {
hato[i] = {- 1 , i};
hako[i].push_back({- 1 , i});
}
map< pair< int , int > , pair< int , int >> memo;
rep(i, Q) {
int t;
cin >> t;
if (t == 1 ) {
int a, b;
cin >> a >> b;
a-- , b-- ;
hato[a] = {i, b};
} else if (t == 2 ) {
int a, b;
cin >> a >> b;
a-- , b-- ;
hako[a].push_back({i, b});
hako[b].push_back({i, a});
} else {
int a;
cin >> a;
a-- ;
auto [id, num] = hato[a];
vector< pair< int , int >> olds;
while (true) {
auto it = upper_bound(all(hako[num]), make_pair(id, INF));
if (it == hako[num].end())
break ;
olds.push_back(* it);
if (memo.count(* it)) {
auto x = memo[* it];
id = x.first;
num = x.second;
} else {
id = it-> first;
num = it-> second;
}
}
if (olds.size())
olds.pop_back();
// 経路圧縮
for (auto [a, b] : olds) {
memo[{a, b}] = {id, num};
}
hato[a] = {id, num};
cout << num + 1 << endl;
}
}
}
解説放送を見たあとの復習
Sat, Mar 1, 2025 E - Xor Sigma Problem https://atcoder.jp/contests/abc365/tasks/abc365_e
$\sum_{i,j} f(i,j)$ 系の問題は $i \leq j$ に関する $f(i,j)$ の値を表に書いてみて規則性を見つけると解けることが多い。
\begin{align}
f(i,j) &= A_i \oplus A_{i+1} \oplus \cdots \oplus A_j \nonumber \\
S_i &= \sum_{j=i}^N f(i,j) \nonumber
\end{align}
と定義する。
表: $f(i,j)$ の値
\begin{align}
\sum_{i=1}^{N-1} \sum_{j=i+1}^N f(i,j) &= \sum_{i=1}^{N} \left\{ \left( \sum_{j=i}^{N} f(i,j) \right) - f(i,i) \right\} \nonumber \\
&= \sum_{i=1}^{N} \left\{ \left( \sum_{j=i}^{N} f(i,j) \right) - A_i \right\} \nonumber \\
&= \sum_{i=1}^{N} S_i - A_i \nonumber
\end{align}
Fri, Feb 28, 2025 E - Distance Sequence https://atcoder.jp/contests/abc253/tasks/abc253_e
$f(i,j)$ を $A_i = j$ となる場合の数とすると
\begin{align}
f(1,j) &= 1 ~~~(\forall j \in [1,M]) \nonumber \\
f(i+1,j) &= \sum_{k=1}^{j-K} f(i,k) + \sum_{k=j+K}^{M} f(i,k) \nonumber
\end{align}
となる。naive に実装すると以下のようになり、計算量が $O(NM^2)$ となるため問題の制約では TLE になる。
vector< vector< mint>> dp(N + 1 , vector< mint> (M + 1 , 0 ));
rep(i, M) dp[1 ][i + 1 ] = 1 ;
rep2(i, 2 , N + 1 ) {
rep2(k, 1 , M + 1 ) {
rep2(j, 1 , M + 1 ) {
if (abs(k - j) >= K)
dp[i][k] += dp[i - 1 ][j];
}
}
}
mint ans = 0 ;
rep2(i, 1 , M + 1 ) ans += dp[N][i];
cout << ans.val() << endl;
ここで dp[i-1] の累積和計算しておくことで一番内側の loop 内の処理を $O(1)$ で行うことができる。
$K = 0$ のときに dp[i-1][j] からの寄与をダブルカウントしないように注意する
Fri, Feb 28, 2025 E - I Hate Sigma Problems https://atcoder.jp/contests/abc371/tasks/abc371_e
sample 2 の $f(i,j)$ の値を表にまとめると以下のようになる.
A_i \ A_j 5 4 2 2 3 2 4 4 1 5 1 2 3 3 4 4 4 4 5 4 1 2 2 3 3 3 3 4 2 1 1 2 2 3 3 4 2 1 2 2 3 3 4 3 1 2 3 3 4 2 1 2 2 3 4 1 1 2 4 1 2 1 1
この表より各行の和の値は以下のように遷移することが推察される。
Mon, Feb 24, 2025 E - Palindromic Shortest Path https://atcoder.jp/contests/abc394/tasks/abc394_e
解説 AC
短い回分から両端に同じ文字を追加していくことで回分の長さを増やしていく。
void solve () {
int n;
cin >> n;
vector< string> delta(n);
rep(i, n) cin >> delta[i];
vvll dist(n, vll(n, - 1 ));
// 回分の最短距離が決まっている path を que に入れる
< pair< int , int >> que;
rep(i, n) {
dist[i][i] = 0 ;
que.push({i, i});
}
rep(i, n) rep(j, n) {
if (i != j && delta[i][j] != '-' ) {
dist[i][j] = 1 ;
que.push({i, j});
}
}
while (que.size()) {
auto [i, j] = que.front();
que.pop();
rep(k, n) {
rep(l, n) {
if (delta[k][i] != '-' && delta[k][i] == delta[j][l] &&
dist[k][l] == - 1 ) {
// i -> j への path の回分の長さはすでに決まっている
// delta[k][i] == delta[j][l] ならば、k -> i -> j -> l という path が回分になる
// que には距離が短い順に入っているので一番最初に見つかった k -> l の path を最短として良い
// k -> i -> j -> l なる path を考えるときに (i,j) の全ての組み合わせを調べる必要はないということ
= dist[i][j] + 2 ;
que.push({k, l});
}
}
}
}
for (auto v : dist)
print(v);
}
Sun, Feb 23, 2025 A. Capitalized? https://atcoder.jp/contests/abc338/tasks/abc338_a
B. Frequency https://atcoder.jp/contests/abc338/tasks/abc338_b
C. Leftover Recipes https://atcoder.jp/contests/abc338/tasks/abc338_c
D. Island Tour https://atcoder.jp/contests/abc338/tasks/abc338_d
解説 AC
void solve () {
ll n, m;
cin >> n >> m;
vll x(m);
rep(i, m) {
cin >> x[i];
x[i]-- ;
}
vll cumsum(n * 2 + 1 , 0 );
rep(i, m - 1 ) {
ll mi = min(x[i], x[i + 1 ]);
ll mx = max(x[i], x[i + 1 ]);
ll dr = mx - mi;
ll dl = n - dr;
cumsum[mi] += dl;
cumsum[mx] -= dl;
cumsum[0 ] += dr;
cumsum[mi] -= dr;
cumsum[mx] += dr;
cumsum[n] -= dr;
}
rep(i, n * 2 ) cumsum[i + 1 ] += cumsum[i];
ll ans = INF;
rep(i, n) chmin(ans, cumsum[i]);
cout << ans << endl;
}
E. Chords https://atcoder.jp/contests/abc338/tasks/abc338_e
Thu, Feb 20, 2025 E - Round Trip https://atcoder.jp/contests/abc276/tasks/abc276_e
start から BFS をする。
start から右移動から始めたところには 1 start から左移動から始めたところには 2 start から上移動から始めたところには 3 start から下移動から始めたところには 4 といった具合に番号を振っていく。(番号が異なれば良いので上下左右と番号の対応が上記と違っても問題ない)
異なる番号が隣り合うところがあれば異なる経路で同じ場所にたどり着けるということなので Yes、そのような場所がなければ No を出力する。
sample 1 の場合の番号の付け方の例は以下のよう
3 3 3 1
-1 3 -1 1
2 0 1 1
2 -1 -1 1
void solve () {
int H, W;
cin >> H >> W;
vector< string> grid(H);
rep(i, H) cin >> grid[i];
int si, sj;
rep(i, H) rep(j, W) if (grid[i][j] == 'S' ) si = i, sj = j;
vvint mark(H, vint(W, - 1 ));
queue< pair< int , int >> q;
q.push({si, sj});
mark[si][sj] = 0 ;
vint di = {0 , 1 , 0 , - 1 };
vint dj = {1 , 0 , - 1 , 0 };
while (q.size()) {
auto [i, j] = q.front();
q.pop();
int c = mark[i][j];
int start = c == 0 ;
rep(d, 4 ) {
if (start)
c = d + 1 ;
int ni = i + di[d], nj = j + dj[d];
if (clamp(ni, 0 , H - 1 ) != ni || clamp(nj, 0 , W - 1 ) != nj)
continue ;
if (grid[ni][nj] == '#' )
continue ;
int m = mark[ni][nj];
if (m > 0 && m != c) {
yesno(true);
return ;
}
if (m == - 1 ) {
mark[ni][nj] = c;
q.push({ni, nj});
}
}
}
yesno(false);
}
Tue, Feb 18, 2025 D - Swap to Gather なんとなく中央の 1 に寄せると良さそうという雰囲気で実装して AC してしまった
void solve () {
int N;
string S;
cin >> N >> S;
vint ids;
rep(i, N) {
if (S[i] == '1' )
ids.push_back(i);
}
ll ans = 0 ;
int mid = ids[ids.size() / 2 ];
int zid = mid + 1 ;
for (int i = mid + 1 ; i < N; i++ ) {
while (S[zid] == '1' && zid < N)
zid++ ;
if (i <= zid)
continue ;
if (S[i] == '1' ) {
ans += i - zid;
swap(S[i], S[zid]);
}
}
zid = mid - 1 ;
for (int i = mid - 1 ; i >= 0 ; i-- ) {
while (S[zid] == '1' && zid >= 0 )
zid-- ;
if (zid <= i)
continue ;
if (S[i] == '1' ) {
ans += zid - i;
swap(S[i], S[zid]);
}
}
cout << ans << endl;
// cout << S << endl;
E - GCD of Subset 愚直に全ての $A_i$ についての約数を調べて出現回数をメモって、各 $i$ に対して $A_i$ の約数のうち出現回数が $K$ を超えている中で最大のものを出力とすると TLE ぎりぎりだがなんとか AC できた。
しかし、どうやら想定解ではなかったらしい。
Sun, Feb 16, 2025 D - Grid and Magnet https://atcoder.jp/contests/abc351/tasks/abc351_d
3時間近くかかったが自力 AC
磁石が置かれていないマスを空マスと呼ぶことにする。
磁石と隣接していない空マス同士を union-find で連結する。
連結部分のサイズと連結部分の外縁にある磁石と隣接する空マスの数の合計のうち最大値を出力する。
int h, w;
vector< string> grid;
vvint memo;
vvint visited;
vint di = {0 , 1 , 0 , - 1 };
vint dj = {1 , 0 , - 1 , 0 };
pair< int , int > ind2sub(int x) {
return {x / w, x % w};
}
int sub2ind (int i, int j) {
return i * w + j;
}
int canMove (int i, int j) {
int ok = 1 ;
rep(d, 4 ) {
int ni = i + di[d], nj = j + dj[d];
if (clamp(ni, 0 , h - 1 ) != ni || clamp(nj, 0 , w - 1 ) != nj)
continue ;
if (grid[ni][nj] == '#' )
ok = 0 ;
}
return ok;
}
void solve () {
cin >> h >> w;
grid = vector< string> (h);
rep(i, h) cin >> grid[i];
dsu uf(h * w);
rep(i, h) rep(j, w) {
if (grid[i][j] == '.' && canMove(i, j)) {
for (auto [ii, jj] : vector< pair< int , int >> ({{1 , 0 }, {0 , 1 }})) {
int ni = i + ii, nj = j + jj;
if (clamp(ni, 0 , h - 1 ) != ni || clamp(nj, 0 , w - 1 ) != nj)
continue ;
if (canMove(ni, nj)) {
uf.merge(sub2ind(i, j), sub2ind(ni, nj));
}
}
}
}
int ans = 1 ;
for (auto v : uf.groups()) {
set< pair< int , int >> stop;
{
auto [i, j] = ind2sub(v[0 ]);
if (grid[i][j] == '#' )
continue ;
else if (! canMove(i, j)) {
continue ;
}
}
for (int id : v) {
auto [i, j] = ind2sub(id);
rep(d, 4 ) {
int ni = i + di[d], nj = j + dj[d];
if (clamp(ni, 0 , h - 1 ) != ni || clamp(nj, 0 , w - 1 ) != nj)
continue ;
if (grid[ni][nj] == '.' && ! canMove(ni, nj))
stop.insert({ni, nj});
}
}
chmax(ans, (int )v.size() + (int )stop.size());
}
cout << ans << endl;
}
Sat, Feb 15, 2025 D - Palindromic Number https://atcoder.jp/contests/abc363/tasks/abc363_d
解説 AC
ll intpow (ll x, ll n) {
long long ret = 1 ;
while (n > 0 ) {
if (n & 1 )
ret *= x;
x *= x;
n >>= 1 ;
}
return ret;
}
void solve () {
ll N;
cin >> N;
if (N == 1 ) {
cout << 0 << endl;
return ;
}
N-- ;
for (ll d = 1 ;; d++ ) {
if (N <= intpow(10 , (d - 1 ) / 2 ) * 9 ) {
ll b = intpow(10 , (d - 1 ) / 2 ) + N - 1 ;
string s = to_string(b);
s.resize(s.size() * 2 - d % 2 , ' ' );
rep(i, d / 2 ) {
s[s.size() - i - 1 ] = s[i];
}
cout << s << endl;
return ;
} else {
N -= intpow(10 , (d - 1 ) / 2 ) * 9 ;
}
}
}
Fri, Feb 14, 2025 D - Divide Interval https://atcoder.jp/contests/abc349/tasks/abc349_d
証明せずに貪欲で AC した。
左端の数から始まる良い数列のうち最長のものを採用していく。
左端の数が $l = 2^i j$ とするとき、良い数列は次の通りである
長さ 数列 $2^i$ $S(2^i j, 2^i (j+1))$ $2^{i-1}$ $S(2^{i-1} 2j, 2^{i-1} 2(j+1))$ $\vdots$ $1$ $S(2^1 2^{i-1}j, 2^1 2^{i-1}(j+1))$ $0$ $S(2^0 2^{i}j, 2^0 2^{i}(j+1))$
このうち $R$ を超えないもので最長のものを採用していく。
void solve () {
ll l, r;
cin >> l >> r;
vector< pair< ll, ll>> ans;
while (r - l >= 1 ) {
ll cnt = 0 ;
while ((l & (1LL << cnt)) == 0 && cnt <= 60 )
cnt++ ;
while (l + (1LL << cnt) > r)
cnt-- ;
ans.push_back({l, l + (1LL << cnt)});
l += 1LL << cnt;
}
cout << ans.size() << endl;
for (auto [x, y] : ans) {
cout << x << ' ' << y << endl;
}
}
Wed, Feb 12, 2025 D - Minimum Steiner Tree https://atcoder.jp/contests/abc368/tasks/abc368_d
$V_1$ から DFS して、子または自身が $V_i$ に含まれていればそのノードを残す。
vvint graph;
vint visited;
set< int > memo;
int ans = 0 ;
bool dfs (int now) {
bool res = false;
if (memo.count(now))
res = true;
for (int nx : graph[now]) {
if (visited[nx])
continue ;
visited[nx] = 1 ;
bool x = dfs(nx);
res = res || x;
// short-circuit で以下のよう書くと dfs が実行されない
// res = res || dfs(nx)
if (res)
ans++ ;
return res;
}
void solve () {
int n, k;
cin >> n >> k;
graph = vvint(n);
rep(i, n - 1 ) {
int u, v;
cin >> u >> v;
u-- , v-- ;
graph[u].push_back(v);
graph[v].push_back(u);
}
vint nodes(k);
rep(i, k) {
cin >> nodes[i];
nodes[i]-- ;
}
for (int x : nodes)
memo.insert(x);
visited = vint(n, 0 );
visited[nodes[0 ]] = 1 ;
dfs(nodes[0 ]);
cout << ans << endl;
}
F - Dividing Game 解説 AC
Wed, Feb 12, 2025 D - Count Bracket Sequences https://atcoder.jp/contests/abc312/tasks/abc312_d
解説 AC
Fri, Feb 7, 2025 D - Only one of two https://atcoder.jp/contests/abc341/tasks/abc341_d
解説 AC
$x$ 以下の整数のうち $N$, $M$ のいずれか一方のみで割り切れるものの個数を $f(x)$ とすると
\begin{align*}
f(x) = \floor{\frac{x}{N}} + \floor{\frac{x}{M}} - 2 \cdot \floor{\frac{x}{\text{lcm}(N, M)}}
\end{align*}
である。
$f(x) \geq K$ となる最小の $x$ を二分探索で求めれば良い。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N, M, K;
cin >> N >> M >> K;
auto f = [& ](ll x) -> ll {
ll numn = x / N;
ll numm = x / M;
ll numc = x / lcm(N, M);
return numn + numm - numc * 2 ;
};
ll wa = 0 , ac = INF;
while (ac - wa > 1 ) {
ll wj = (ac + wa) / 2 ;
if (f(wj) >= K)
ac = wj;
else
wa = wj;
}
cout << ac << endl;
}
E - Alternating String https://atcoder.jp/contests/abc341/tasks/abc341_e
Thu, Feb 6, 2025 D - Three Days Ago 解説 AC
void solve () {
string S;
cin >> S;
int n = S.size();
vvll v(n + 1 , vll(10 , 0 ));
rep(i, n) {
v[i + 1 ][S[i] - '0' ]++ ;
}
rep(k, 10 ) {
rep(i, n) {
v[i + 1 ][k] += v[i][k];
v[i + 1 ][k] %= 2 ;
}
}
vll cnt(1 << 10 , 0 );
rep2(i, 0 , n + 1 ) {
int x = 0 ;
rep(k, 10 ) {
x *= 2 ;
if (v[i][k])
x += 1 ;
}
cnt[x]++ ;
}
ll ans = 0 ;
rep(i, 1 << 10 ) {
ans += cnt[i] * (cnt[i] - 1 ) / 2 ;
}
cout << ans << endl;
}
Tue, Feb 4, 2025 D - Pyramid https://atcoder.jp/contests/abc336/tasks/abc336_d
解説 AC.
void solve () {
ll N;
cin >> N;
vll A(N);
rep(i, N) cin >> A[i];
A.push_back(0 );
A.insert(A.begin(), 0 );
N += 2 ;
vll dl(N, 0 ), dr(N, 0 );
rep2(i, 1 , N) {
dl[i] = min(dl[i - 1 ] + 1 , A[i]);
}
rep(i, N - 1 ) {
int k = N - 1 - i;
dr[k - 1 ] = min(dr[k] + 1 , A[k - 1 ]);
}
ll ans = 0 ;
rep(i, N) {
chmax(ans, min(dr[i], dl[i]));
}
cout << ans << endl;
}
E - Digit Sum Divisible 桁 DP の問題とわかった状態で自力 AC.
Tue, Feb 4, 2025 E - Grid Filling https://atcoder.jp/contests/abc278/tasks/abc278_e
$\mathrm{ rows }(i, m)$ を 行番号が $[0,i)$ の範囲(0-index)での数字 $m$ の出現回数、$\mathrm{ cols }(j,m)$ を列番号が $[0,i)$ の範囲での数字 $m$ の出現回数とする。
$[i,i+h)$, $[j,j+w)$ の領域が塗りつぶされたときに、残りのマスに数字 $m$ の出現する場合以下の式の少なくとも1つが true となる。
\begin{align}
&\mathrm{ cols }(j-1,m) > 0 \\
&\mathrm{ cols }(W,m) - \mathrm{ cols }(j+w-1,m)) > 0 \\
&\mathrm{ rows }(i-1,m) > 0 \\
&\mathrm{ rows }(H, m) - \mathrm{ rows }(i+h-1,m) > 0
\end{align}
eq (1): 塗りつぶしたマスより左側の領域に対応 eq (2): 塗りつぶしたマスより右側の領域に対応 eq (3): 塗りつぶしたマスより上側の領域に対応 eq (4): 塗りつぶしたマスより下側の領域に対応 出現する数字は $[1,300]$ の範疇なので愚直に全通り出現するか確認し、出現した数の種類数を出力する。
Tue, Feb 4, 2025 A - mod M Game 2 解説 AC だが、かなり解像度が低い。
$\displaystyle \sum_{k=1}^{N} k = \frac{1}{2}N(N+1)$ より両者のカードの総和は $N(N+1)$。
最後の Bob の出す手が $b$ のとき Alice が最後に出した手までの総和は $N(N+1) - b$。
$N(N+1) - b$ が $0$ にできたら Bob の勝ち、それ以外のときは Alice の勝ち。
\begin{align}
N(N+1) - b &\equiv 0 \mod M \\
N(N+1) &\equiv b \mod M \\
\end{align}
$b \in [1,N]$ より、$1 \leq (N(N+1) \mod M) \leq N$ のときは Bob の勝ち。それ以外のときは Alice の勝ち
Mon, Feb 3, 2025 D - M<=ab https://atcoder.jp/contests/abc296/tasks/abc296_d
解説 AC。
条件より $X = ab \wedge X \geq M$ である。また $a,b$ は対称だから $a \leq b$ としても答えは変わらない。
\begin{align}
M \leq X &= ab \Leftrightarrow \nonumber \\
\frac{M}{a} &\leq b \nonumber \\
\biggl\lceil \frac{M}{a} \biggr\rceil &\leq b \nonumber \\
\end{align}
$\lceil M/a \rceil$ は $b$ の下界だから $a \leq b$ と合わせて
\begin{align}
&a \leq \biggl\lceil \frac{M}{a} \biggr\rceil \nonumber < \frac{M}{a} + 1 \nonumber \\
\Leftrightarrow ~ &a(a-1) < M \nonumber
\end{align}
Sun, Feb 2, 2025 D - Factorial and Multiple https://atcoder.jp/contests/abc280/tasks/abc280_d
解説 AC
ルジャンドルの定理と二分探索で解く
ref: 予備ノリ 一度聞いたら忘れない『ルジャンドルの定理』の授業
ll f (ll n, ll p) {
ll ans = 0 ;
ll b = p;
while (n / b) {
ans += n / b;
b *= p;
}
return ans;
}
void solve () {
ll K;
cin >> K;
vector< pair< ll, ll>> div;
{
ll x = K;
for (ll i = 2 ; i * i <= x; i++ ) {
if (x % i != 0 )
continue ;
ll cnt = 0 ;
while (x % i == 0 ) {
x /= i;
cnt++ ;
}
div.emplace_back(i, cnt);
}
if (x != 1 )
div.emplace_back(x, 1 );
}
ll ac = K, wa = 1 ;
while (abs(ac - wa) > 1 ) {
ll wj = (ac + wa) / 2 ;
ll ok = 1 ;
for (auto [p, cnt] : div) {
if (f(wj, p) < cnt)
ok = 0 ;
}
if (ok)
ac = wj;
else
wa = wj;
}
cout << ac << endl;
}
Sun, Feb 2, 2025 D - Buildings 解説 AC.
void solve () {
ll n;
cin >> n;
vll h(n);
rep(i, n) cin >> h[i];
vll ans(n);
vll st;
for (int i = n - 1 ; i >= 0 ; i-- ) {
ans[i] = st.size();
while (st.size() != 0 && st.back() < h[i]) {
st.pop_back();
}
st.push_back(h[i]);
}
print(ans);
}
E - K-th Largest Connected Components https://atcoder.jp/contests/abc372/tasks/abc372_e
解説 AC
void solve () {
ll N, Q;
cin >> N >> Q;
dsu uf(N);
vvint nodes(N);
rep(i, N) {
nodes[i].push_back(i);
}
rep(i, Q) {
int q, a, b;
cin >> q >> a >> b;
if (q == 1 ) {
int u = a - 1 , v = b - 1 ;
if (uf.same(u, v))
continue ;
int ou = uf.leader(u);
int ov = uf.leader(v);
int newl = uf.merge(u, v);
vint tmp = nodes[ou];
for (auto x : nodes[ov])
tmp.push_back(x);
sort(rall(tmp));
vint newv;
for (int i = 0 ; i < 10 && i < tmp.size(); i++ ) {
newv.push_back(tmp[i]);
}
nodes[newl] = newv;
} else {
int v = a - 1 , k = b;
int l = uf.leader(v);
if (nodes[l].size() >= k) {
cout << nodes[l][k - 1 ] + 1 << endl;
} else {
cout << - 1 << endl;
}
}
}
}
Sun, Feb 2, 2025 A - Not coprime https://atcoder.jp/contests/arc114/tasks/arc114_a
50 以下の素数は15個である。
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
これらの積は $10^{18}$ 以下なので答えは long long int で収まる。
\begin{align*}
\prod_{p \in \text{50 以下の素数}} p = 614,889,782,588,491,410 < 10^{18}
\end{align*}
考えうる $Y$ の値はせいぜい $2^{15} - 1 = 32767$ 個なので全ての組み合わせを試して条件にあうもののうちの最小を求めれば良い。
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vll X(N);
rep(i, N) cin >> X[i];
vint used(55 );
for (ll x : X) {
ll t = x;
rep2(i, 2 , t + 1 ) {
if (x % i == 0 ) {
used[i] = 1 ;
while (x % i == 0 ) x /= i;
}
}
}
vll primes;
rep(i, 50 ) {
if (used[i]) primes.push_back(i);
}
ll ans = INF;
int sz = primes.size();
rep(state, 1ll << sz) {
ll t = 1 ;
rep(i, sz) {
if ((state >> i) & 1 ) t *= primes[i];
}
int ok = 1 ;
for (ll x : X) {
if (gcd(t, x) == 1 ) {
ok = 0 ;
break ;
}
}
if (ok) chmin(ans, t);
}
cout << ans << endl;
}
B - Special Subsets 条件より $i$ から $f(i)$ に辺を張ったグラフを作り、このうちサイクルを成しているサブグラフの頂点集合が $T$ になる。
各サブグラフは独立しているからサイクルを成しているサブグラフの個数を $n$ とすると $2^n - 1$ が答え。
Sun, Feb 2, 2025 E - Mex and Update https://atcoder.jp/contests/abc330/tasks/abc330_e
解説 AC
Sun, Feb 2, 2025 E - Destruction https://atcoder.jp/contests/abc218/tasks/abc218_e
$C_i$ が小さい順にクラスカル法で最小全域木を作る。
使わない辺のうち、コストが負のものは捨てて、コストが正のものを答えとして計上していく。
計上しない負のコストの辺はグラフから取り除かずそのままにしている辺に相当する。
void solve () {
ll N, M;
cin >> N >> M;
vector< Edge> es(M);
rep(i, M) {
ll a, b, c;
cin >> a >> b >> c;
a-- , b-- ;
es[i] = {a, b, c};
}
priority_queue< Edge, vector< Edge> , greater< Edge>> pq;
for (auto e : es)
pq.push(e);
dsu uf(N);
vll dust;
while (pq.size()) {
auto [u, v, c] = pq.top();
pq.pop();
if (uf.same(u, v)) {
if (c > 0 )
dust.push_back({c});
} else {
uf.merge(u, v);
}
}
ll ans = 0 ;
for (ll x : dust) {
if (x > 0 )
ans += x;
}
cout << ans << endl;
}
Sun, Feb 2, 2025 D - Gravity https://atcoder.jp/contests/abc391/tasks/abc391_d
嘘解法で通してしまった。$x$ が同じ時ブロックではあとからのほうが $y$ が大きいとしてしまったがそんな制約はなかった。
$y$ に sort 入れなかったときにバグる入力例
4 2
1 2
1 1
2 1
2 2
2
1 2
1 3
解法 列 $x$ のあるブロックのうち下から $j$ 番目のブロックの $y$ 座標を $y_{x,j}$ とする。
$k$ 回目の行が消える操作は $t_k = \max \\{ y_{x,k} | x \in [1,W], x \in \mathbb{Z} \\}$ の時刻に実行される。
このような $y_{x,k}$ が存在しない場合は $t_k = \infty$ とする。
ブロック $i$ が 列 $X_i$ の下から k 番目のブロックであるとき、消えるのは時刻 $t_k$ のときである。
これらの情報からクエリの時刻においてブロック $i$ が存在しているかどうかを判定する。
Fri, Jan 31, 2025 D - A Piece of Cake ピースの数は多いので愚直に全探索はできない。
イチゴが入るピースの数は少ないので各イチゴがどのピースに入るかという基準で考える。
イチゴが入るピースの右下の座標をそのピースの代表としてそのピースに入るイチゴの数を数えばよい。イチゴがどのピースに属するかはそのイチゴのすぐ右と下にある分割線を二分探索で探せば良い。
void solve () {
ll W, H, N;
cin >> W >> H >> N;
vll p(N), q(N);
rep(i, N) {
cin >> p[i] >> q[i];
}
ll na;
cin >> na;
vll a(na + 1 );
rep(i, na) {
cin >> a[i];
}
a.back() = W;
ll nb;
cin >> nb;
vll b(nb + 1 );
rep(i, nb) {
cin >> b[i];
}
b.back() = H;
// イチゴが入るピースの右下の座標
< pair< ll, ll> , ll> cnt;
rep(i, N) {
ll rh, rw;
rh = * lower_bound(all(a), p[i]);
rw = * lower_bound(all(b), q[i]);
cnt[{rh, rw}]++ ;
}
// ピースの数が最大数より少なかったらイチゴが 0 個のピースを sentinel
// として一つ追加
if ((ll)cnt.size() < (na + 1 ) * (nb + 1 ))
cnt[{- 1 , - 1 }] = 0 ;
ll maxv = 0 , minv = INF;
for (auto it = cnt.begin(); it != cnt.end(); it++ ) {
chmin(minv, it-> second);
chmax(maxv, it-> second);
}
cout << minv << ' ' << maxv << endl;
}
Fri, Jan 31, 2025 D - Popcount and XOR 考察 自力で解けたが1日考えた。
$c = \mathrm{popcount}(C)$ とする。$a$X \oplus Y = C$ のことは一旦忘れ $\mathrm{popcount}(X) = a, \mathrm{popcount}(Y) = b$ だけを考える。
$X$, $Y$ で極力同じ場所の bit を立てた場合 $\mathrm{popcount}(X \oplus Y) = |a-b|$。
$X$, $Y$ で同じ場所に bit を建てなかった場合 $\mathrm{popcount}(X \oplus Y) = a+b$ であるから $X \oplus Y = C$ になる必要条件は
$$
|a-b| \leq c \leq a+b
$$である。また同じ場所に立っていた bit を別の場所で立てた場合 popcount の値は2ずつ変わるので $a+b$ と $c$ の parity は同じにならなければならない。
たとえば、下記のように $X$ の 2 bit 目の bit を下げて 4 bit 目を上げると xor を取ると popcount の値が2増える。逆に $X,Y$ のどちらかだけに立っていた bit の位置を1つの場所に移動させると popcount の値が 2 減る。
Fri, Jan 31, 2025 D - General Weighted Max Matching $N$ が奇数のとき、頂点を一つ追加してその頂点との辺の重みは $0$ としても結果は変わらない。よって以後 $N$ は偶数として扱う。
2頂点ずつ $N/2$ 組に分ける組み合わせの数は
$$
\frac{\binom{n}{2} \times \binom{n-2}{2} \times \cdots \times \binom{2}{2}}{2^{N/2} (N/2)!}
$$である。$N=16$ のとき $\displaystyle \frac{16!}{2^8 8!} = 2,027,025$ なので全探索しても十分間に合う。
実装をどうするかを考える。まずは $N = 4$ という具体例について考えてみる。
このときの分け方は次の3通りが考えられる。
$(1, 2), (3, 4)$ $(1, 3), (2, 4)$ $(1, 4), (2, 3)$ これより
まだ選んでいないものから一番 index が若いものを選ぶ 相方はそれ以降の index からまだ選んでいないものを選ぶ 次の組についても同様にして選んで行く N/2 組みできた時点で終了する という再帰関数を書けば全探索ができる。
ll N, m;
vvll D (16 , vll(16 , 0 ));
ll ans = 0 ;
void dfs (int state, int depth, ll sum) {
if (depth == (N + 1 ) / 2 ) {
chmax(ans, sum);
}
int l = 0 ;
rep(i, m) if (! (state & (1 << i))) {
l = i;
state ^= (1 << i);
break ;
}
rep2(i, l + 1 , m) {
if (! (state & (1 << i))) {
state ^= (1 << i);
dfs(state, depth + 1 , sum + D[l][i]);
state ^= (1 << i);
}
}
}
void solve () {
cin >> N;
m = N + N % 2 ;
rep(i, N) {
rep2(j, i + 1 , N) {
cin >> D[i][j];
}
}
dfs(0 , 0 , 0 );
cout << ans << endl;
}
E - Sandwiches https://atcoder.jp/contests/abc318/tasks/abc318_e
Wed, Jan 29, 2025 D - Marking 方針がなかなか決まらなくて諦めかけたがなんとか自力 AC。
$x_k$ を $k$ 番目に印をつけられるマスの番号とする。
すでに印がつけられていたとしても i の操作で移動したとすると
\begin{align}
x_1 &= 0 \nonumber \\
x_2 &= x_1 + D \mod N \nonumber \\
x_3 &= x_2 + D \mod N \nonumber \\
\vdots \nonumber \\
x_k &= x_{k-1} + D \mod N \nonumber \\
\end{align}
これより、$x_k = x_1 + (k-1)D \mod N$ ということがわかる。
操作 ii が初めて起こるのは $\alpha D \equiv 0 \mod N$ となる最小の正の整数 $\alpha$ のときである。すなわち、$\alpha D$ が $N$ の倍数となるような最小の正の整数 $\alpha$ を見つけることができれば周期がわかる。よって操作 ii が何回行われたのかもわかる。
Wed, Jan 29, 2025 E - Clique Connect https://atcoder.jp/contests/abc352/tasks/abc352_e
最小全域木を構成するアルゴリズムであるクラスカル法を思いつけると解ける。
クラスカル法は辺のコストが小さい順に閉路ができないように辺を採用していくアルゴリズムである。
$C_i$ が小さい部分集合から辺を構成し順にクラスカル法で辺を張っていく。このとき、部分集合内の頂点同士が連結になりさえすれば良いので
$\\{(A_1, A_j)| j \in [2, K_i], j \in \mathbb{Z} \\}$ という辺だけを考えるだけで良い。
最終的に連結グラフになっていたらそのコストを出力し、なってなかったら $-1$ を出力する。
void solve () {
ll N, M;
cin >> N >> M;
vvll A(M);
vll C(M);
rep(i, M) {
ll k, c;
cin >> k >> c;
C[i] = c;
rep(j, k) {
ll a;
cin >> a;
a-- ;
A[i].push_back(a);
}
}
vector< pair< ll, int >> cs;
rep(i, M) {
cs.push_back({C[i], i});
}
sort(all(cs));
dsu uf(N);
ll ans = 0 ;
for (auto [c, i] : cs) {
int k = A[i].size();
rep2(j, 1 , k) {
int a = A[i][0 ], b = A[i][j];
if (uf.same(a, b))
continue ;
uf.merge(a, b);
ans += c;
}
}
if (uf.groups().size() != 1 )
ans = - 1 ;
cout << ans << endl;
}
Wed, Jan 29, 2025 B - New Place https://atcoder.jp/contests/arc154/tasks/arc154_b
$S$ の $i$ 文字目、$T$ の $j$ 文字目をそれぞれ $s_i$, $t_j$ と書くことにする。
削除した文字は一旦プールに入れておくということにする。
後ろから文字を比較していって
一致した場合 一致しなかった場合プールにある場合 プールにない場合その文字を調達してこないといけないので調達したい文字を含めて $S$ の先頭の文字を削除する 削除した回数をカウントしつつ、削除した文字はプールに入れておく。ただし調達対象の文字はプールに入れない 次の文字を比較する void solve () {
int N;
cin >> N;
string S, T;
cin >> S >> T;
ll ans = 0 ;
map< char , int > store;
int tl = N - 1 , sh = 0 , sl = N - 1 ;
while (tl >= 0 && sl >= 0 && sh <= sl) {
if (S[sl] == T[tl]) {
tl-- , sl-- ;
} else if (store[T[tl]]) {
store[T[tl]]-- ;
tl-- ;
} else {
while (sh <= sl) {
ans++ ;
if (S[sh] == T[tl]) {
sh++ , tl-- ;
break ;
} else {
store[S[sh]]++ ;
sh++ ;
}
}
if (sh > sl) {
cout << - 1 << endl;
return ;
}
}
}
cout << ans << endl;
}
Wed, Jan 29, 2025 D - Max Multiple https://atcoder.jp/contests/abc281/tasks/abc281_d
$dp(i,j,r)$ を $i$ 番目までの数字から $j$ 個使ってできた総和を D で割った余りが $r$ のときの総和の最大値とする
void solve () {
ll N, K, D;
cin >> N >> K >> D;
vll A(N + 1 );
rep(i, N) cin >> A[i + 1 ];
// dp[i][j][r]: i 番目までの数字から j 個を選んだときの和を D
// で割ったあまりが r のときの和の最大値
< vvll> dp(N + 1 , vvll(K + 1 , vll(D, - INF)));
dp[0 ][0 ][0 ] = 0 ;
rep2(i, 1 , N + 1 ) {
rep(j, K + 1 ) {
// i 番目の数字を使わない
= dp[i - 1 ][j];
// i 番目の数字を使う
if (j > 0 ) {
rep(r, D) {
if (dp[i - 1 ][j - 1 ][r] < 0 )
continue ;
ll x = dp[i - 1 ][j - 1 ][r] + A[i];
chmax(dp[i][j][x % D], x);
}
}
}
}
ll ans = dp[N][K][0 ];
if (ans < 0 )
ans = - 1 ;
cout << ans << endl;
}
Wed, Jan 29, 2025 E - Set Meal https://atcoder.jp/contests/abc331/tasks/abc331_e
解説 AC
2025/2/23 retry
副菜を降順にソートしておく。主菜を固定したときに選べる副菜のうち一番高いものを採用する。全ての主菜に対して同じことをしてそのうちの最大を出力。
選ぶ必要のない副菜の検索を飛ばすことで $N+L$ 回程度の比較しかされないので十分早い。
void solve () {
ll n, m, l;
cin >> n >> m >> l;
vll a(n), b(m), c(l), d(l);
rep(i, n) cin >> a[i];
rep(i, m) cin >> b[i];
rep(i, l) {
cin >> c[i] >> d[i];
c[i]-- , d[i]-- ;
}
vector< pair< ll, int >> B;
rep(i, m) B.push_back({b[i], i});
sort(rall(B));
set< pair< int , int >> ban;
rep(i, l) ban.insert({c[i], d[i]});
ll ans = 0 ;
rep(i, n) {
rep(j, m) {
if (! ban.count({i, B[j].second})) {
chmax(ans, a[i] + B[j].first);
break ;
}
}
}
cout << ans << endl;
}
Wed, Jan 29, 2025 D - Keep Distance https://atcoder.jp/contests/abc382/tasks/abc382_d
$1 \leq x \leq y \leq z \leq 6$ を満たす $(x,y,z)$ の組み合わせを求めるのと同じ要領で解ける。
\begin{align}
x^\prime &= x \nonumber \\
y^\prime &= y+1 \nonumber \\
z^\prime &= z+2 \nonumber
\end{align}
とすると $1 \leq x^\prime < y^\prime < z^\prime \leq 8$ となる。
$(x^\prime, y^\prime, z^\prime)$ が決まると $(x,y,z)$ も一通りに決まるから $(x^\prime, y^\prime, z^\prime)$ の組み合わせを調べれば良い。
やることとしては $1 \sim 8$ までの数字から重複なく3つ選び小さい方から順に $(x^\prime, y^\prime, z^\prime)$ とすれば良い。
実際の問題について考える
\begin{align}
&A_1 + 10 \leq A_2 \Rightarrow A_1 \leq A_2 - 10 < A_2 - 9 \nonumber \\
&A_2 + 10 \leq A_3 \Rightarrow A_2 - 9 \leq A_3 - 19 \Rightarrow A_2 - 9 < A_3 - 18 \nonumber \\
&\vdots \nonumber
\end{align}
Mon, Jan 27, 2025 D - Hidden Weights $u_i \rightarrow v_i$ への辺の重みは $w_i$, $v_i \rightarrow u_i$ への辺を $-w_i$ で張り適当なところを $0$ でスタートして新たに訪問したノードに重みに応じて値をおいていく。
負の重みの辺を追加するのがミソ
struct Edge {
ll to, weight;
};
void dfs (vector< vector< Edge>>& graph, vll& ans, int now) {
for (auto [to, w] : graph[now]) {
if (ans[to] != INF)
continue ;
ans[to] = ans[now] + w;
dfs(graph, ans, to);
}
}
void solve () {
int N, M;
cin >> N >> M;
vll u(M), v(M), w(M);
rep(i, M) {
cin >> u[i] >> v[i] >> w[i];
u[i]-- , v[i]-- ;
}
vector< vector< Edge>> graph(N);
rep(i, M) {
graph[u[i]].push_back({v[i], w[i]});
graph[v[i]].push_back({u[i], - w[i]});
}
vll ans(N, INF);
rep(i, N) {
if (ans[i] == INF) {
ans[i] = 0 ;
dfs(graph, ans, i);
}
}
print(ans);
}
Sun, Jan 26, 2025 A - Replace Digits https://atcoder.jp/contests/arc191/tasks/arc191_a
コンテスト中考えていたこと $T$ を降順に sort して $S$ が大きくなる限りは $T$ の文字に置き換えていく。改変後の $S$ を $S^\prime$ とする。
余った文字はすでに置き換えた文字の元々あった場所より、余った文字の元々の index が小さければその文字を捨てる(捨てる文字を先に差し込んでからあとから置き換え対象の文字で上書きできるので捨てても問題ない)。それもできなかったら余った文字の中で元々の index が一番後ろとなるものを $S^\prime$ の最後の文字に置き換えればいいと思った。
提出して WA になった。
https://atcoder.jp/contests/arc191/submissions/62131491
このケースだと $S = 912, T = 111$ というケースにおいて $S = 911$ となってしまうが $S$ の 1 のところに $T$ の 1 で置き換えることで最終的に $S = 912$ のままにできる。
よって index の考慮に加えてすでに $S$ の中にある文字も捨てて良い。これで AC した
void solve () {
int N, M;
cin >> N >> M;
string S, T;
cin >> S >> T;
vector< pair< char , int >> t;
rep(i, M) t.push_back({T[i], i});
sort(rall(t));
set< int > used;
int i = 0 , j = 0 ;
while (i < N && j < M) {
if (S[i] < t[j].first) {
S[i] = t[j].first;
used.insert(t[j].second);
i++ ;
j++ ;
} else {
i++ ;
}
}
if (j < M) {
set< char > freq;
for (char c : S)
freq.insert(c);
rep2(k, j, M) {
if (freq.count(t[k].first)) {
used.insert(t[k].second);
continue ;
}
auto it = used.lower_bound(t[k].second);
if (it != used.end()) {
continue ;
}
S[N - 1 ] = t[k].first;
used.insert(t[k].second);
}
}
cout << S << endl;
}
https://atcoder.jp/contests/arc191/submissions/62132625
Sun, Jan 26, 2025 I - Coins $dp(i,num)$ を $i$ 番目までのコインを投げたときに表が num 枚となる確率とすると
\begin{align*}
dp(i,num) &+= dp(i-1,num-1) \times p_i \\
dp(i,num-1) &= dp(i-1,num-1) \times (1 - p_i) \\
dp(0,0) &= 1
\end{align*}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vector< double > p(N);
rep(i, N) cin >> p[i];
// dp[i][num]: i 枚目まで見て表の枚数が num 枚となる確率
+ 1 , vector< double > (N + 1 ));
dp[0 ][0 ] = 1.0 ;
rep2(i, 1 , N + 1 ) {
double pi = p[i - 1 ];
for (int num = N; num > 0 ; num-- ) {
dp[i][num] += dp[i - 1 ][num - 1 ] * pi;
dp[i][num - 1 ] = dp[i - 1 ][num - 1 ] * (1.0 - pi);
}
}
double ans = 0.0 ;
rep2(num, (N + 1 ) / 2 , N + 1 ) {
ans += dp[N][num];
}
printf("%.15lf \n " , ans);
}
void solve () {
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
ll N;
cin >> N;
vector< double > p(N);
rep(i, N) cin >> p[i];
// dp[i]: 表の枚数が i 枚となる確率
< double > dp(N + 1 );
dp[0 ] = 1.0 ;
for (auto pi : p) {
for (int num = N; num > 0 ; num-- ) {
dp[num] += dp[num - 1 ] * pi;
dp[num - 1 ] *= (1.0 - pi);
}
}
double ans = 0.0 ;
rep2(i, (N + 1 ) / 2 , N + 1 ) {
ans += dp[i];
}
printf("%.15lf \n " , ans);
}
L - Deque https://atcoder.jp/contests/dp/tasks/dp_l
Sat, Jan 25, 2025 B - Geometric Sequence https://atcoder.jp/contests/abc390/tasks/abc390_b
等比数列の問題
解き方が思いつかなくてテンパった。
$\lfloor \frac{A_{i+1}}{A_i} \rfloor$ を $i = 1\sim N-1$ ですべて一致するか見ようとしたが項比が非整数のときに対応できなくてサンプルでまず落ちる。項比を double で扱ったとしても 999999998 999999999 1000000000 のような数列のときに誤差のせいで $\frac{999999998}{999999999} == \frac{999999999}{1000000000}$ が true を返してしまう。
有理数だったらちゃんと比較できるのだけれどもということを思いついてようやく整数演算で確かめる方法を思いついた。
$\displaystyle \frac{A_{i+1}}{A_{i}} = \frac{A_{i+2}}{A_{i+1}} \rightarrow A_{i+1}^{2} = A_{i} A_{i+2}$ が成り立っているかを確かめればいい
void solve () {
ll N;
cin >> N;
vector< double > v(N);
rep(i, N) {
cin >> v[i];
}
if (N <= 2 ) {
yesno(true);
return ;
}
rep(i, N - 2 ) {
ll a = v[i], b = v[i + 1 ], c = v[i + 2 ];
if (b * b != a * c) {
yesno(false);
return ;
}
}
yesno(true);
}
C - Paint to make a rectangle 黒マスがある行番号の最小値、最大値をそれぞれ $i_{\mathrm{ min }}, i_{\mathrm{ max }}$ とし, 黒マスのある列番号の最小値、最大値をそれぞれ $j_{\mathrm{ min }}, j_{\mathrm{ max }}$ とする。
Sat, Jan 25, 2025 https://atcoder.jp/contests/abc366
D - Cuboid Sum Query 3次元累積和の問題
https://atcoder.jp/contests/abc366/tasks/abc366_d
$f_i(a,b) = \sum_{i=a}^{b}$ とする。
\begin{align}
\sum_{i=a}^{x} &\sum_{i=b}^{y} \sum_{i=c}^{z} \nonumber = f_i(a,x)f_j(b,y)f_k(c,z) \nonumber \\
&= \left\{ f_i(1,x) - f_i(1,a-1) \right\} \nonumber \\
&~~~ \times \left\{ f_j(1,y) - f_j(1,b-1) \right\} \nonumber \\
&~~~ \times \left\{ f_k(1,z) - f_k(1,c-1) \right\} \nonumber \\
&= f_i(1,x)f_j(1,y)f_k(1,z) - f_i(1,x)f_j(1,y)f_k(1,c-1) \nonumber \\
&~~~ - f_i(1,x)f_j(1,b-1)f_k(1,z) + f_i(1,x)f_j(1,b-1)f_k(1,c-1) \nonumber \\
&~~~ - f_i(1,a-1)f_j(1,y)f_k(1,z) + f_i(1,a-1)f_j(1,y)f_k(1,c-1) \nonumber \\
&~~~ + f_i(1,a-1)f_j(1,b-1)f_k(1,z) - f_i(1,a-1)f_j(1,b-1)f_k(1,c-1) \nonumber \\
\end{align}
Sun, Jan 19, 2025 C https://atcoder.jp/contests/abc389/tasks/abc389_c
deque にヘビの頭の座標と長さを入れる。
タイプ2 で全体の要素の座標を更新すると要素数分更新する必要があるので非効率。出ていったヘビの長さを記録しておき、あとからその値を引く
タイプ1 のときは最後尾のヘビの座標が $x$, 長さが $L$ のときは $(x+L, l)$ を deque に追加する タイプ2 のとき、先頭のヘビの座標と長さが $(x,l)$ のとき $sub = x+l$ と記録しつつ、先頭のヘビを deque から抜く。deque にいるヘビの数が 0 のときは $sub = 0$ にする タイプ3 のとき $deque[k].first - sub$ を出力する void solve () {
ll Q;
cin >> Q;
ll sub = 0 ;
// head pos, length
< pair< ll, ll>> que;
rep(i, Q) {
ll x;
cin >> x;
if (x == 1 ) {
ll l;
cin >> l;
if (que.size()) {
auto [prevpos, prevlen] = que.back();
que.push_back({prevpos + prevlen, l});
} else {
que.push_back({0 , l});
}
} else if (x == 2 ) {
auto [pos, len] = que.front();
que.pop_front();
sub = pos + len;
if (que.empty())
sub = 0 ;
} else { // x==3
cin >> k;
k-- ;
cout << que[k].first - sub << endl;
}
}
}
D https://atcoder.jp/contests/abc389/tasks/abc389_d
Sat, Jan 11, 2025 D - Coming of Age Celebration https://atcoder.jp/contests/abc388/tasks/abc388_d
0-index で考える。$i$ 番目の宇宙人が成人したときにもらう石の数を $C_i$ とし、 $i$ 番目の宇宙人がこれから成人する宇宙人に渡す石の数を $D_i$ とすると $D_i = \min(A_i + C_i, N - i - 1)$ である。
$i$ 番目の宇宙人が最終的に持っている石の数は $A_i + C_i - D_i$ になる。
$C_i$ の管理方法を工夫することでこの問題を解く。
$i$ 番目の宇宙人が何番目の宇宙人にまで石を配るかを考えると $i+D_i$ 番目の宇宙人にまで石を配ることになる。この数を multiset に保存していく。
$j > i$ 番目の人がもらう石の数は $ j \leq x, x \in multiset$ を満たす $x$ の個数と一致する。$j$ 番目の人のときに $x < j$ となる要素は意味がないから予め消しておくと multiset の大きさが $j$ 番目の宇宙人がもらう石の数に等しくなる。これにより $C_j$ が求まる。$C_j$ が求まれば $D_j$ も決まるので、$D_j > 0$ ならば $j + D_j$ を multiset に入れる。これにより答えが求まる。
Fri, Jan 10, 2025 D https://atcoder.jp/contests/abc254/tasks/abc254_d
命題1 $i \times j \text{ が平方数} \leftrightarrow \frac{i\times j}{f(i) \times f(j)} \text{ が平方数}$
($\rightarrow$)
$i \times j$ が平方数であるから $i \times j$ は以下のようにかける。
$$
i \times j = \prod_{k} p^{2r_k}_{k}
$$ここで、$p_k$ は素数であり、$r_k$ は非負整数。
$f(i)$, $f(j)$ も平方数であるから
$$
f(i) = \prod_{k} p^{2n_{k}}_{k}
$$$$
f(j) = \prod_{k} p^{2m_{k}}_{k}
$$とかける。ここで $n_k$, $m_k$ は非負整数。
よって
$$
\frac{i\times j}{f(i) \times f(j)} = \prod_{k} p^{2(r_k - n_k - m_k)}_k
$$であるから、因数が偶数となるため平方数。
$(\leftarrow)$
$\frac{i\times j}{f(i) \times f(j)}$ が平方数であるから、$\frac{i\times j}{f(i) \times f(j)} = x^2$ となるある正の整数 $x$ が存在する。
同様にして $f(i) = y^2, f(j) = z^2$ とかける。ここで $y, z$ は正の整数.
Sun, Dec 22, 2024 C - Doukasen 解説の解説
ぶつかる地点を $x$ とする。左端から $x$ まで行く時間を $t_l$, 右端から $x$ まで行く時間を $t_r$ とすると当たり前だが $t_l = t_r$ が成り立つ。
一方、 左端からだけ燃やしたときにすべてが燃えるのにかかる時間は $T = \sum^{N}_{i=1}\frac{A_i}{B_i}$ である。
$t = t_l$ とすると $2t = T$ であるから
$t = \frac{1}{2} \sum_{i=1}^{N}\frac{A_i}{B_i}$
である。
Sun, Apr 10, 2022 A - Move Right 問題
$0 s_0 s_1 s_2$ を出力すればよい
void solve () {
string s;
cin >> s;
cout << 0 << s.substr(0 , 3 ) << endl;
}
提出コード
B - Unique Nicknames 人 $i$ について, 次の条件 $P$, $Q$ のうちいずれかが成り立っていればその人にあだ名をつけることは可能である.
P: $s_i$ をニックネームとして選んだとき, 全ての $i \neq j$ に対して $s_i \neq s_j \wedge s_i \neq t_i$ Q: $t_i$ をニックネームとして選んだとき, 全ての $i \neq j$ に対して $s_i \neq s_j \wedge s_i \neq t_i$ これが全ての人に対して調べる.
void solve () {
int n;
cin >> n;
vector< string> S(n), T(n);
rep(i, n) cin >> S[i] >> T[i];
rep(i, n) {
int ok = 1 ;
rep(j, n) {
if (i == j)
continue ;
if (S[i] == S[j] || S[i] == T[j])
ok = 0 ;
}
if (ok)
continue ;
ok = 1 ;
rep(j, n) {
if (i == j)
continue ;
if (T[i] == S[j] || T[i] == T[j])
ok = 0 ;
}
if (! ok) {
cout << "No" << endl;
return ;
}
}
cout << "Yes" << endl;
}
提出コード
Sat, Apr 2, 2022 A - Four Points 問題
辺が $x$ 軸に平行または $y$ 軸に平行であるから, 長方形を構成する4点に関して
$x$ 座標が同じ点が2つずつ, $y$ 座標が同じ点が2つずつある.
この問題では3点が与えられるので残る1点の座標は
$x$ 座標: 3点の $x$ 座標の XOR $y$ 座標: 3点の $y$ 座標の XOR となる.
提出コード
B - Get Closer 問題
$(A, B)$ 方向への単位ベクトルを求めれば良いので $\displaystyle \left(\frac{A}{\sqrt{A^2 + B^2}}, \frac{B}{\sqrt{A^2 + B^2}} \right)$ が答え.
提出コード
C - Coupon 問題
まず各商品に対して $\frac{A_i}{X}$ 枚のクーポンを使う. クーポンが足りなくなったらそのまま.
クーポンが余った場合, 各商品に払わないといけない金額は $X$ 未満になっているので, 残高が高い順にクーポンを適用させていけばよい.
提出コード
D - 2-variable Function 問題
$f(a,b) = a^3 + a^2b + ab^2 + b^3$ とする.
$f(a,b) \geq N$ を満たす最小の $f(a, b)$ を求める.
Sat, Mar 12, 2022 ##
[問題]()
[提出コード]()
A - Shampoo 問題
単純にシミュレーションをするか, $V <= A+B+C$ のときは3人が1順するごとに $A+B+C$ 減るので
$V$ を V % (A + B + C) スタートにしても問題ない.
この状況で誰が使うときに不足するかを調べればよい.
void solve () {
int v, a, b, c;
cin >> v >> a >> b >> c;
v %= a + b + c;
if (v - a < 0 ) {
cout << "F" << endl;
return ;
}
v -= a;
if (v - b < 0 ) {
cout << "M" << endl;
return ;
}
cout << "T" << endl;
}
提出コード
Sun, Mar 6, 2022 A - T-shirt 問題
$X \leq A$ なら 1 $X > B$ なら 0 それ以外なら $\displaystyle \frac{C}{B-A}$ を出力
提出コード
B - Minimize Ordering 問題
文字を昇順に並べ替えたものが答え
提出コード
C - 1111gal password 問題
$dp[i][x]$: $i$ 桁の整数で, $i$ 桁目が $x$ である問題の条件を満たす整数の場合の数とする.
また初期状態として $\forall x, dp[1][x] = 1$ とする.
$i$ 桁の整数で $i$ 桁目が $x$ となるような整数の場合の数は
$i-1$ 桁目の数と $x$ の差の絶対値が1以下となるような $i-1$ 桁の整数の数の合計であるから
dp[i][x] += dp[i-1][x]
if (x-1 >= 1) dp[i][x] += dp[i-1][x-1]
if (x+1 <= 9) dp[i][x] += dp[i-1][x+1]
となる.
Sun, Feb 27, 2022 A - Digit Machine 問題
a[a[a[0]]] を出力すれば良い.
void solve () {
vint a(10 );
rep(i, 10 ) cin >> a[i];
cout << a[a[a[0 ]]] << endl;
}
提出コード
B - Pasta 問題
map にそれぞれの麺の長さの数を保存して, $i$ 日目に麺が残っていたら 1 decrement,
残っていなかったら No を出力.
最終的に $M$ 日間の食事計画に問題なければ Yes を出力.
提出コード
C - Connect 6 問題
$(i, j)$ を始点として上下左右斜め8方向に対して6マスの中に白の数が2つ以下となっているかを全探索する.
方向が違う以外は調べる処理の中身は同じなので関数化しておくと楽.
bool search (int i, int j, int di, int dj) {
// (i, j): start point
// (fi, fj): final point
int fi = i + di * 5 ;
int fj = j + dj * 5 ;
if (fi < 0 || fi >= n || fj < 0 || fj >= n)
return false;
int rem = 6 ;
int r = i, c = j;
int numwhite = 0 ;
rep(i, rem) {
numwhite += grid[r][c] == '.' ;
r += di;
c += dj;
}
if (numwhite <= 2 ) {
return true;
}
return false;
}
提出コード
Sun, Feb 27, 2022 A - A ↔ BB 問題
文字列のうち A or B が連続する区間はいったん全ての A を BB にして
その区間の文字を B のみからなるようにした後に先頭から近い方の BB を A に変換していくのを繰り返すのが最適.
例
CABAC -> CBBBBBC -> CAABC
模範解答を見て知ったが string(n, 'A') とすると A が $n$ 文字の並んだ文字列を生成できるらしい.
またどうやら C++ の string で str1 += str2 とするのは str2 の長さ分を加える計算量しか掛からないっぽい.
str1 += str2 は str1 に push_back で str2 の要素を1個ずつ入れるのと計算量としては変わらないっぽい.
string string_cancat (int n) {
string s = "" ;
rep(i, n) s += ('a' + (i % 5 ));
return s;
}
void test (int n) {
clock_t t = clock();
string s = string_cancat(n);
double time = (double )(clock() - t) / CLOCKS_PER_SEC;
printf("n = %10d: \t time = %.9lf sec \n " , n, time);
}
void solve () {
int n = 10 ;
while (n < 100000000 ) {
test(n);
n *= 10 ;
}
}
n = 10: time = 0.000002000 sec
n = 100: time = 0.000009000 sec
n = 1000: time = 0.000013000 sec
n = 10000: time = 0.000090000 sec
n = 100000: time = 0.000807000 sec
n = 1000000: time = 0.012396000 sec
n = 10000000: time = 0.049614000 sec
提出コード
Sun, Feb 20, 2022 A - Edge Checker 問題
$|a-b| = 1$ または $a = 1, b = 10$ のときは Yes, それ以外のときは No
提出コード
B - Count Distinct Integers 問題
$N$ 個の要素全部 set に突っ込んで最後に size を出力
提出コード
C - Jumping Takahashi 問題
$dp[i][x]$ を $i$ 回目のジャンプで座標 $x$ に行けるかとし
初期値 $dp[0][0] = true$ とする.
$dp[i-1][x] = true$ ならば $dp[i][x+a] = dp[i][x+b] = true$ に更新する.
提出コード
D - Strange Balls 問題
筒の中に入っているボールの数を同じ数字が書かれたボールに関しては圧縮してもつ.
筒の中に [2, 3, 3, 2, 4, 4, 4, 5] と入っていたら
[{2, 1}, {3, 2}, {2, 1}, {4, 3}, {5, 1}] という風に {数字, 個数} として保持する.
Sat, Feb 19, 2022 A - Horizon 問題
問題分通りの値を出力するだけ.
提出コード
B - Integer Division 問題
$X > 0$ のときは素直に整数除算 $X / 10$ を出力する.
$X < 0$ のとき, $X \equiv 0 \mod 10$ なら整数除算 $X / 10$ を出力し,
$X % 10 \neq 0$ なら $X / 10 - 1$ を出力する.
void solve () {
ll x;
cin >> x;
if (x < 0 && x % 10 != 0 ) {
cout << x / 10 - 1 << endl;
} else {
cout << x / 10 << endl;
}
}
余談
Sun, Feb 13, 2022 A - Floor, Ceil - Decomposition 数字 $x$ をそのままにするか, $\lfloor \frac{x}{2} \rfloor$, $\lceil \frac{x}{2} \rceil$ に書き換えるかは
$x < \lfloor \frac{x}{2} \rfloor \times \lceil \frac{x}{2} \rceil$ となれば書き換えたほうが全体の積が大きくなり,
その他の場合は $x$ のままにするのがよい.
おおよそ $\displaystyle \left\lfloor \frac{x}{2} \right\rfloor \times \left\lceil \frac{x}{2} \right\rceil \approx \frac{x^2}{4}$ となることを考え,
$y = x$ と $y = \frac{x^2}{4}$ のグラフを描くと $0 \leq x \leq 4$ の区間では $y = x$ が,
$x > 4$ の区間では $y = x^2 / 4$ のほうが大きいことがわかる.
$g(x) = \max(x, \left\lfloor \frac{x}{2} \right\rfloor \times \left\lceil \frac{x}{2} \right\rceil)$ とすると
Tue, Feb 1, 2022 C - kasaka https://atcoder.jp/contests/abc237/tasks/abc237_c
先頭にある連続する a の数を $x$, 末尾に連続する a の数を $y$ とすると
$x > y$ のとき, どうやっても回文にはできない.
それ以外のとき, 先頭と末尾の a を消して残った文字が回文になっていれば Yes, そうでなければ No.
初め以下のようなコードを書き AC を取れてしまったが, これは嘘解法.
void solve () {
string s;
cin >> s;
int l = 0 , r = (int )s.size() - 1 ;
while (l < r) {
// 頭に a を追加する
if (s[l] != 'a' && s[r] == 'a' ) {
r-- ;
} else if (s[l] == s[r]) {
l++ ;
r-- ;
} else {
cout << "No" << endl;
return ;
}
}
cout << "Yes" << endl;
return ;
}
axyaxa という文字列のとき上のプログラムだと Yes を出力するが, 本来は No を出力すべき
Tue, Feb 1, 2022 A - Exponential or Quadratic 問題
愚直に $2^n$ を計算すると $n$ が最大で $10^9$ のためオーバーフローする.
$n$ が十分大きいところでは $2^n > n^2$ となるため, そのようなところを探す.
$n = 1$: $2^n = 2 > 1 = n^2$ $n = 2$: $2^n = 4 = 4 = n^2$ $n = 3$: $2^n = 8 < 9 = n^2$ $n = 4$: $2^n = 16 = 16 = n^2$ $n = 5$: $2^n = 32 > 25 = n^2$ $n = 6$: $2^n = 64 > 36 = n^2$ $\vdots$ $n = 2, 3, 4$ のときは題意は false であるがそれ以外では true となる.
Sat, Jan 29, 2022 A - Bridge and Sheets すでに敷いたシートの右端を $r$ とすると, $r < x$ となる $x$ までをカバーするのに必要なシーツの枚数は
$\displaystyle \left\lceil \frac{x-r}{W} \right\rceil$ である.
これをひたすら繰り返す
提出コード
B - Reserve or Reverse $l = 1, r = N$ として以下を繰り返すと辞書順最小になる
$[l,r]$ の範囲にある文字のうち $s_l$ 未満の最小の文字のうちで一番右側のあるものの index を $r^\prime$ とすると $s_l$ と $s_{r^\prime}$ を交換し $r = r^\prime - 1$ に更新する. そのようなものがない場合は $l$ をインクリメントする $l \geq r$ となったら終了する. void solve () {
int n;
cin >> n;
string s;
cin >> s;
vvint a(26 );
rep(i, n) {
a[s[i] - 'a' ].push_back(i);
}
int l = 0 , r = n - 1 ;
while (l < r) {
// [l,r] の範囲にある文字のうち s[l] 未満の最小の文字のうちで一番右側にあるものの index を探す
int ok = 0 ;
rep(c, 26 ) {
if (s[l] - 'a' <= c)
break ;
// 右端以上になっている要素は消す
while (! a[c].empty() && a[c].back() > r)
a[c].pop_back();
// 一つも要素がない or 左端より小さい値しかなかったら交換できないので飛ばす
if (a[c].empty() || a[c].back() < l)
continue ;
r = a[c].back();
ok = 1 ;
break ;
}
if (ok) {
swap(s[l], s[r]);
r-- ;
}
l++ ;
}
cout << s << endl;
}
$r^\prime$ の探し方を二分探索で探すという方法もある.
Sun, Jan 23, 2022 B - Who is missing? 問題
出現回数が3回の数字を出力すればよい.
愚直に解くと以下のようになる. これで AC は一応取れる.
void solve () {
int n;
cin >> n;
vint card(n + 1 );
rep(i, 4 * n - 1 ) {
int a;
cin >> a;
card[a]++ ;
}
rep2(i, 1 , n + 1 ) {
if (card[i] != 4 )
cout << i << endl;
}
}
別解
数字 $x$ を XOR で偶数回作用させると 0 になり, 奇数回作用させると $x$ になることを思い出すと,
出力すべき数字だけ奇数回だけ出現するので, $XOR(A_1, A_2, \cdots, A_{4N-1})$ が答えとなる.
void solve () {
int n;
cin >> n;
int x = 0 ;
rep(i, 4 * n - 1 ) {
int y;
cin >> y;
x ^= y;
}
cout << x << endl;
}
tourist の提出コード を見てこの解放を知った.
Sun, Jan 23, 2022 A - Erase by Value 問題
$A_i > A_{i+1}$ となる最初の $A_i$ を消したときが辞書順最小となる.
$A_i < A_{i+1}$ となる $A_i$ を消した場合, 辞書順であとにくる数列に変化してしまうので数列が広義単調増加しているうちはその文字は消すべきではない.
B - Dividing Subsequence 問題
LCS の亜種. 「$b_i$ は $a_i$ の倍数」という条件を $a_i = b_i$ に変えると LCS と同じになる.
ただし, LCS を使うと計算量が $O(N^2)$ になってしまうので, そのままでは適用することができない.
$Q_j$ が $P_i$ の倍数となるような index のペア $(i,j)$ に関して,
第1要素で昇順, 第2要素で降順に並べたものに対して, 第2要素の LIS の長さを求めると問題の答えになる.
入力例を使って実際に考えてみる.
3 1 4 2
4 2 1 3
このとき, ペアを辺と捉えると下図のようになる.
ここで, 辺を交差しないようにできるだけ多く選択したい.
第1要素を横軸, 第2要素を縦軸に辺をプロットすると下図のようになる.
これより, 2辺 $(a_i, b_i)$, $(a_j, b_j)$ が交差しないための条件は $a_i < a_j \wedge b_i < b_j$ が成り立つことである.
この条件を満たすように辺を選んだときの, 選べる辺の最大値は先に述べたように第2要素の LIS の長さとなる.
Sun, Jan 16, 2022 D - Multiply and Rotate 問題
操作1: $x$ を $a$ 倍する 操作2: $x$ を文字列とみなして, 末尾の数字を先頭に移動させる
とする. DFS or BFS を使って, 1 からスタートして N になるまでの操作回数の最小値を求める. $N$ からスタートして $1$ にする方でも可.
DFS の計算量の正確な見積もり方はわからないが, $\log_2(10^6) = 19.93...$ であるので, 7桁の数を $a$ で割れる回数は高々20回程度で
操作2をしたところでそんなにパターン数は多くなさそうに思えるが, 本当にそうなのか微妙なところ.
際どいテストケース持ってこられたときに TLE にならないか自信がない.
E - MST + 1 問題
クエリを先読みする問題.
元々のグラフの辺と, クエリによる辺を合わせて最小全域木を作ることを考える.
作っている際にクエリ由来の辺を使ったほうが得なときは, そのクエリを Yes, そうでない場合は No を出力する.
プリム法だとグラフの構築が必要になるので, クラスカル法で解くほうが楽そう.
Mon, Jan 10, 2022 問題
$dp[i][x]$: $i$ 番目までの数字を使う, かつ, $A_i$ を $x~(x = + \text{ or } -)$ とするような式の合計とする.
具体的に書いてみるとわかりやすいが, 遷移は以下のようになる.
\begin{align}
dp[i][+] &= (dp[i-1][+] + dp[i-1][-]) + (i-1 \text{ までを使ったときの式の場合の数}) \times A_i \
dp[i][-] &= dp[i-1][+] - (A_{i-1} \text{を足したときの式の場合の数}) \times A_i
\end{align}
掛け合わせる数はフィボナッチ数列になっている. $DP$ テーブル一つだけで処理するのは面倒(pair を使って合計と個数を記録していればできる)なので掛ける数は別にテーブルに保持しておくと楽
void solve () {
int n;
cin >> n;
vector< ll> a(n + 1 );
rep(i, n) cin >> a[i + 1 ];
vector< vector< mint>> dp(n + 1 , vector< mint> (2 , 0 )), mul(n + 1 , vector< mint> (2 , 0 ));
dp[1 ][0 ] = a[1 ];
mul[1 ][0 ] = 1 ;
rep2(i, 2 , n + 1 ) {
mul[i][0 ] = mul[i - 1 ][0 ] + mul[i - 1 ][1 ];
mul[i][1 ] = mul[i - 1 ][0 ];
dp[i][0 ] = dp[i - 1 ][0 ] + dp[i - 1 ][1 ] + mul[i][0 ] * a[i];
dp[i][1 ] = dp[i - 1 ][0 ] - mul[i][1 ] * a[i];
}
cout << (dp[n][0 ] + dp[n][1 ]).val() << endl;
}
提出コード
Sun, Jan 9, 2022 A - Gold and Silver 問題
$i$ 日目に金を銀に, $j$ 日目に銀を金に交換すると金の量は $A_i / A_j$ 倍になる.
ここで
$$
\frac{A_i}{A_j} = \frac{A_i}{A_{i+1}} \times \frac{A_{i+1}}{A_{i+2}} \times \cdots \times \frac{A_{j-1}}{A_j}
$$であるから $i$ 日目に金を銀に, $j$ 日目に銀を金に交換することは
$A_i / A_{i+1}$$i$ 日目に金を銀に交換 $i+1$ 日目に銀を金に交換 $A_{i+1} / A_{i+2}$$i+1$ 日目に金を銀に交換 $i+2$ 日目に銀を金に交換 … $A_{j-1} / A_j$$j-1$ 日目に金を銀に交換 $j$ 日目に銀を金に交換 することと等価である. 金の量を増やすには $A_i > A_{i+1}$ となるところで交換を行えばいい.
void solve () {
int n;
cin >> n;
vector< int > A(n), change(n, 0 );
rep(i, n) cin >> A[i];
rep(i, n - 1 ) {
if (A[i] > A[i + 1 ]) {
change[i] ^= 1 ;
change[i + 1 ] ^= 1 ;
}
}
print(change);
}
XOR をとっているのは同じ日に金を銀に, 銀を金にという交換を連続する操作があった場合に
打ち消し合わせるため.
Sun, Jan 9, 2022 B - Range Point Distance 問題
$dist(l, r, x) = \max(0, l-x, x-r)$ であるから
\begin{align}
\max(dist(L_1, R_1, x)&, \cdots, dist(L_k, R_k, x)) \
&= \max(0, L_1 - x, x - R_1, \cdots, L_k - x, x - R_k) \
&= \max(0, \max(L_1 - x, \cdots, L_k - x), \max(x - R_1, \cdots, x - R_k))
\end{align}
である.
\begin{align}
&\max(L_1 - x, \cdots, L_k - x) = \max(L_1, \cdots, L_k) - x = A_k - x\
&\max(x - R_1, \cdots, x - R_k) = x + \max(-R_1, \cdots, -R_k) = x - \min(R_1, \cdots, R_k) = x - B_k
\end{align}
where $A_k = \max(L_1, \cdots, L_k)$ and $B_k = \min(R_1, \cdots, R_k)$.
Sat, Jan 8, 2022 C - Happy New Year 問題
$K$ を2進数にしたときの 1 となっているところを 2 に置き換えたものが答え
void solve () {
ll k;
cin >> k;
// n: bit が立っている最も大きい idx
int n = 0 ;
rep(i, 60 ) if ((k >> i) & 1 ) n = i;
string ans = "" ;
rep(i, n + 1 ) ans.push_back((k >> i) & 1 ? '2' : '0' );
reverse(all(ans));
cout << ans << endl;
}
提出コード
D - Prefix K-th Max $S = \{P_1, \cdots, P_K\}$ となる集合を考える.
$K+1$ 番目以降の数は保存しておく必要がないので, $P_{K+1} > \min(S)$ ならば $\min(S)$ を取り除き, $P_{K+1}$ を追加.
$P_{K+1} < \min(S)$ ならば $P_{K+1}$ は集合に入れずそのまま捨てる.
以降 $P_N$ まで同様の操作を行って, その時その時の $\min(S)$ を出力する.
Tue, Jan 4, 2022 D - Between Two Arrays 問題
$dp[i][x]$: $i$ 番目までの数が決まっており, $c_i = x$ のときの場合の数とする.
$c_i = x$ となるときの場合の数は, $c_{i-1} \leq x$ となる場合の数であるから
$\displaystyle dp[i][x] = \sum_{k = a_{i-1}}^x dp[i-1][k]$
これを元に naive に実装すると以下のようになる.
vector< vector< ll>> dp(n, vector< ll> (MAX, 0 ));
rep2(x, a[0 ], b[0 ] + 1 ) dp[0 ][x] = 1 ;
rep2(i, 1 , n) {
rep2(x, a[i], b[i] + 1 ) {
rep2(k, a[i - 1 ], x + 1 ) {
dp[i][x] += dp[i - 1 ][k];
dp[i][x] %= MOD;
}
}
}
ll ans = 0 ;
rep(i, MAX) {
ans += dp[n - 1 ][i];
ans %= MOD;
}
cout << ans << endl;
しかしこれでは最大で $O(N \times 3000^2) = O(3000^3)$ の計算量がかかり制限時間に待ち合わない.
TLE 提出コード
Mon, Dec 27, 2021 C - Product 問題
$\displaystyle \prod^N_{i=1}L_i \leq 10^5$ より, 考えうるボールの取り出し方を全通り試しても $O(10^5)$ なので全探索する.
$1 \leq a_{i,j} \leq 10^9$ と $N \geq 2$ より, $10^9$ という数が3回以上掛けることがありうるが, 倍精度整数で表現できる整数の範囲はたかだか18桁なので愚直に積を取ると途中でオーバーフローしてしまう.
掛け算をしている途中で $X < \text{(それまでの積)} \times a_{i,j}$ としたいがこのままだと右辺がオーバーフローする可能性があるので, $X / \text{(それまでの積)} < a_{i,j}$ とする.
void dfs(int depth, ll prod) {
if (depth == N) {
if (prod == X) ans++;
return;
}
for (ll x : a[depth]) {
// X < x*prod
if (X / prod < x) continue;
dfs(depth+1, prod*x);
}
}
このオーバーフロー対策を入れないと
Mon, Dec 27, 2021 A - Permutation Grid 問題
1-index で考え, grid の $A$ と呼ぶことにする.
公式解説 の通り, $R$, $C$ の並び方がともに $1, 2, \cdots, n$ である場合は, 上から $r$ 行目, $c$ 行目のマスが $r+c \geq n + 1$ である場合に黒で, それ以外では白となる.
ここで行 $i$, $j$ を入れ替えたとき $C_1, \cdots, C_n$ の結果に影響を与えない.
同様に列 $i$, $j$ を入れ替えたとき $R_1, \cdots, R_n$ の結果に影響を与えない.
$R_i$, $C_i$ が昇順になるように行・列の入れ替えを行ってできる grid を $A^\prime$ としたとき $A$ の $(r, c)$ 成分が $A^\prime$ のどの成分に対応するか調べることでマスが黒か白か判定できる.
$R$, $C$ は $1, \cdots, n$ の順列だから, ソートによって $r$ 行目は $R_r$ 行目に, $c$ 列目は $C_c$ 列目に移動する.
よって $R_r + C_c \geq n+1$ のとき黒, それ以外のときは白となる.
Thu, Dec 23, 2021 A - QQ solver 問題
char で受けて '0' で引くということもできるが, iostream は条件に合うものを最大長マッチでとってくる(らしい)ので下のような書き方でも通る.
int a, b;
char x;
cin >> a >> x >> b;
cout << a*b << endl;
提出コード
C - Graph Isomorphism 問題
高橋くんの番号と青木くんの番号の対応関係 $N!$ 通りをすべて試して, グラフが一致すれば Yes, だめなら No.
提出コード
D - Weak Takahashi 問題
$(1, 1)$ から BFS してステップ数が最大となるものが答え
提出コード
E - Rook Path 問題
$H \times W$ のグリッドを下のような領域に分ける.
$S_{0,0} = \{(x, y) | x \neq x_2 \wedge y \neq y_2 \}$ (白の領域) $S_{0,1} = \{(x, y_2) | x \neq x_2\}$ (赤の領域) $S_{1,0} = \{(x_2, y) | y \neq y_2\}$ (青の領域) $S_{1,1} = \{(x_2, y_2)\}$ (緑の領域)
Sun, Dec 12, 2021 C - Counting 2 昇順でソートして lower_bound 使って $x_i$ 以上となる index を調べる.
二部探索用途で multiset を使うと遅いので注意.
ref: multiset vs vector
submission code
D - Neighbors 人を node, 隣り合う人の情報を edge としグラフを構築する.
node の次数が3以上のとき, またはグラフに cycle がある場合は No, それ以外は Yes を出力する.
submission code: cycle 検出方法ごとの実装
Union Find 辺を作る前に両端の node が同じ親を持っているか確認する. 同じだった場合, 辺を張ると cycle を作ってしまうことがわかる. 1
|
2 -- 3
1-2, 2-3 の辺を張った状態で 1, 3 のそれぞれの親を調べると同じになる. その場合, 1-3 に辺を張ると cycle ができることがわかる.
Sun, Dec 12, 2021 int <-> string to_string(int) -> stringto_string(ll) -> stringstoi(string) -> intstoll(string) -> llpriority queue 昇順
#include <iostream>
#include <queue>
int main () {
// intを要素に持つ優先順位付きキュー.
// 降順に処理する
:: priority_queue< int > que;
// データを追加する
3 );
que.push(1 );
que.push(4 );
// 処理順に出力する
while (! que.empty()) {
std:: cout << que.top() << std:: endl;
que.pop();
}
}
4
3
1
降順に出力
#include <iostream>
#include <queue>
int main () {
// intを要素に持つ優先順位付きキュー.
// 降順に処理する
:: priority_queue< int , vector< int > , greater< int >> que;
// データを追加する
3 );
que.push(1 );
que.push(4 );
// 降順順に出力する
while (! que.empty()) {
std:: cout << que.top() << std:: endl;
que.pop();
}
}
1
3
4
struct で priority queue
Sun, Dec 12, 2021 入出力の高速化 他人のコードをみてたまにやっているのを見かける以下のような書き方は入出力を高速化するためにやっているらしい
ios_base:: sync_with_stdio(false);
cin.tie(nullptr );
cout << val << '\n' ;
ref: https://maspypy.com/library-checker-many-a-b#google_vignette
multiset vs vector multiset は遅いので二部探索のように使うときは注意する.
insert, find, erase の計算量は $\log(N)$ ($N$ は要素数)であるが, 定数項が効いているのかなかなかに遅い.
#include <bits/stdc++.h>
#define all(v) (v).begin(), (v).end()
#define rall(v) (v).rbegin(), (v).rend()
#define rep(i, n) for (int i = 0; i < (n); ++i)
#define rep2(i, k, n) for (int i = (k); i < (n); ++i)
using namespace std;
using ll = long long ;
using P = pair< int , int > ;
// using P = pair<ll,ll>;
const ll INF = (ll)1e18 ;
// const int INF = (int)1e9+7;
template < typename T>
void chmin(T& a, T b) {
a = min(a, b);
}
template < typename T>
void chmax(T& a, T b) {
a = max(a, b);
}
void solve () {
int ns[] = {100 , 1000 , 10000 , 100000 , 1000000 , 10000000 };
cout << "multiset" << endl;
cout << "size \t elapsed time (sec)" << endl;
for (int n : ns) {
multiset< int > ms;
clock_t start = clock();
rep(i, n) ms.insert(i);
clock_t end = clock();
cout << n << " \t " << (double )(end - start) / CLOCKS_PER_SEC << endl;
}
cout << endl;
cout << "vector" << endl;
cout << "size \t elapsed time (sec)" << endl;
for (int n : ns) {
vector< int > v(n);
clock_t start = clock();
rep(i, n) v[i] = i;
sort(all(v));
clock_t end = clock();
cout << n << " \t " << (double )(end - start) / CLOCKS_PER_SEC << endl;
}
}
int main () {
solve();
return 0 ;
}
multiset
size elapsed time (sec)
100 9e-06
1000 6.4e-05
10000 0.000915
100000 0.011328
1000000 0.144224
10000000 2.5446
vector
size elapsed time (sec)
100 5e-06
1000 1e-05
10000 7.5e-05
100000 0.000858
1000000 0.010139
10000000 0.130072
Sat, Dec 4, 2021 E - Fraction Floor Sum $\displaystyle \sum^{n}_{i=1} \floor{N/i}$ を求める問題.
言い換えると $y \le n / x$, $(1 \le x \le n)$ の範囲にある格子点の数を数える問題.
$$
\sum_{i=1}^{n} \floor{N/i} = 2 \sum_{i=1}^{\floor{\sqrt{n}}} \floor{N/i} - (\floor{\sqrt{n}})^2
$$計算量は $O(\sqrt{n})$ で解ける.
解説 $y = n/x$ は $y = x$ に関して対称であり, $y = n/x$ と $y = x$ は $(x,y) = (\sqrt{n}, \sqrt{n})$ で交わる.
対称性より図の青い斜線の領域に含まれる格子点の数 ($\sum^{\floor{\sqrt{n}}}_{i = 1}\floor{N/i}$) と, 赤い斜線の領域に含まれる格子点の数は一致する. 2つの領域で共通する部分に含まれる格子点の数は $(\floor{\sqrt{n}})^2$.
したがって,
$$
\begin{aligned}
(\mathrm{題意の格子点数}) \\\\
=& (\mathrm{青斜線に含まれる格子点数}) + (\mathrm{赤斜線に含まれる格子点数}) - (共通する領域に含まれる格子点数) \\\\
=& 2\sum^{\floor{\sqrt{n}}}_{i = 1}\floor{ N/i } - (\floor{ \sqrt{n} })^2
\end{aligned}
$$
Mon, Jan 1, 0001