ABC 230

Table of Contents

E - Fraction Floor Sum

$\displaystyle \sum^{n}_{i=1} \floor{N/i}$ を求める問題. 言い換えると $y \le n / x$, $(1 \le x \le n)$ の範囲にある格子点の数を数える問題.

$$ \sum_{i=1}^{n} \floor{N/i} = 2 \sum_{i=1}^{\floor{\sqrt{n}}} \floor{N/i} - (\floor{\sqrt{n}})^2 $$

計算量は $O(\sqrt{n})$ で解ける.

解説

$y = n/x$ は $y = x$ に関して対称であり, $y = n/x$ と $y = x$ は $(x,y) = (\sqrt{n}, \sqrt{n})$ で交わる.

対称性より図の青い斜線の領域に含まれる格子点の数 ($\sum^{\floor{\sqrt{n}}}_{i = 1}\floor{N/i}$) と, 赤い斜線の領域に含まれる格子点の数は一致する. 2つの領域で共通する部分に含まれる格子点の数は $(\floor{\sqrt{n}})^2$.

したがって,

$$ \begin{aligned} (\mathrm{題意の格子点数}) \\\\ =& (\mathrm{青斜線に含まれる格子点数}) + (\mathrm{赤斜線に含まれる格子点数}) - (共通する領域に含まれる格子点数) \\\\ =& 2\sum^{\floor{\sqrt{n}}}_{i = 1}\floor{ N/i } - (\floor{ \sqrt{n} })^2 \end{aligned} $$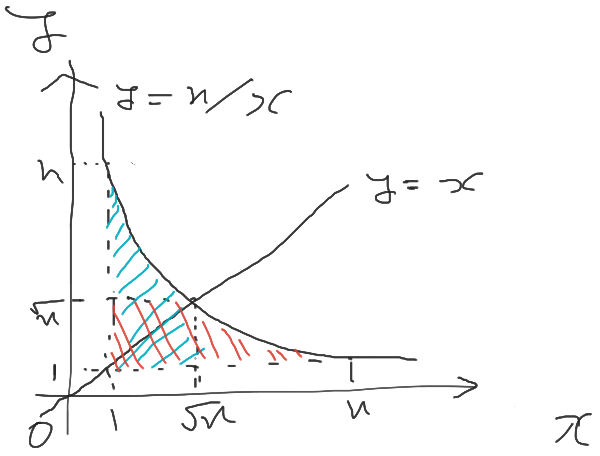

e.png

#include <cmath>
#include <iostream>
using namespace std;
using ll = long long;

#define rep(i, n) for (ll i = 0; i < (n); i++)

int main(int argc, char* argv[]) {
    ll n;
    cin >> n;

    ll sqr = sqrt(n);
    ll ans = 0;
    for (ll i = 1; i <= sqr; i++) {
        ans += n / i;
    }
    ans *= 2;
    ans -= sqr * sqr;
    cout << ans << endl;

    return 0;
}

submissions code

Reference