ABC 232
Table of Contents
A - QQ solver
char で受けて '0' で引くということもできるが, iostream は条件に合うものを最大長マッチでとってくる(らしい)ので下のような書き方でも通る.
int a, b;
char x;
cin >> a >> x >> b;
cout << a*b << endl;
C - Graph Isomorphism
高橋くんの番号と青木くんの番号の対応関係 $N!$ 通りをすべて試して, グラフが一致すれば Yes, だめなら No.
D - Weak Takahashi
$(1, 1)$ から BFS してステップ数が最大となるものが答え
E - Rook Path
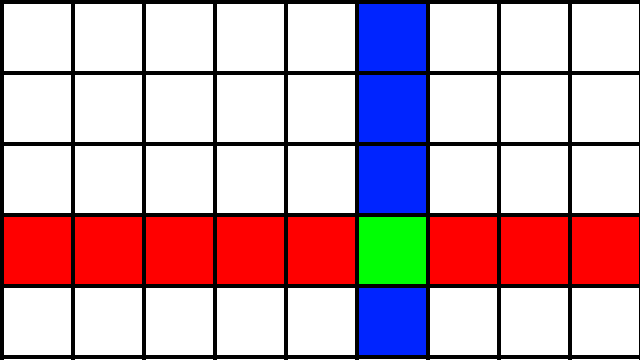
$H \times W$ のグリッドを下のような領域に分ける.
- $S_{0,0} = \{(x, y) | x \neq x_2 \wedge y \neq y_2 \}$ (白の領域)
- $S_{0,1} = \{(x, y_2) | x \neq x_2\}$ (赤の領域)
- $S_{1,0} = \{(x_2, y) | y \neq y_2\}$ (青の領域)
- $S_{1,1} = \{(x_2, y_2)\}$ (緑の領域)
$dp[k][i][j]$ を $k$ 回の操作のあとで領域 $S_{i,j}$ にいる場合の数とすると
- $dp[k][0][0] = (W-1)dp[k-1][0][1] + (H-1)dp[k-1][1][0] + (H + W -4)dp[k-1][0][0]$
- 赤の領域にいるとき上下の $W-1$ 通りのマスの移動ができる
- 青の領域にいるとき左右の $H-1$ 通りのマスの移動ができる
- 白の領域にいるとき上下左右から青と赤の領域に重ねる部分を覗いた $H+W-4$ 通りのマスの移動ができる
- $dp[k][0][1] = dp[k-1][0][0] + (H-2)dp[k-1][0][1] + (H-1)dp[k-1][1][1]$
- 白の領域から赤の領域に行く方法は1通り
- 赤の領域から他の赤の領域に行く方法は $H-2$ 通り
- 緑の領域から赤の領域に行く方法は $H-1$ 通り
- $dp[k][1][0] = dp[k-1][0][0] + (W-2)dp[k-1][1][0] + (W-1)dp[k-1][1][1]$
- 上の場合と同様
- $dp[k][1][1] = dp[k-1][0][1] + dp[k-1][1][0]$
- 赤の領域から緑の領域に行く方法は1通り
- 青の領域から緑の領域に行く方法は1通り
※ 上記の説明の○通りは特定の領域の特定のマスからの移動の場合の数について述べている.
上の式を見ると連立方程式になっている. 次のように行列を使って表現することができる. $v_i(t)$ を時刻 $t$ における領域 $i$ ($i = 2a+b$, $S_{a,b}$) にある状態数, 遷移行列 $T = \begin{bmatrix}H+W-4 & W-1 & H-1 & 0 \\ 1 & H-2 & 0 & H-1 \\ 1 & 0 & W-2 & W-1 \\ 0 & 1 & 1 & 0\end{bmatrix}$ とすると $K$ 回後の操作のあとの状態ベクトル $\vec{v}(K)$ は $\vec{v}(K) = T^K \vec{v}(0)$ となる. $v_3(K)$ が問題の答えとなる.
$T^K$ の計算や高速冪乗計算の要領で高速に計算できる.
F - Simple Operations on Sequence
swap と数の増減の操作は独立なので操作の順番は結果に依存しない.
$A$ の並べ替えによってできた数列を $A^\prime$ とし, $A^\prime_i$ を $i = 1$ から順に決めていくことを考える.
$dp[i][S]$ を $i$ 番目までが確定しており, 1番目から $i$ 番目に含まれる数字の集合が $S = \{A^\prime_1, \cdots, A^\prime_i\}$ となるようなときの最小コストとする.
例:
$dp[2][\{A_3, A_7\}] = \min(A_3 A_7 ... \text{となるような swap のコスト} + \text{数の増減}, A_3 A_7 ... \text{となるような swap のコスト} + \text{数の増減})$.
$A_j$ $(j \notin S)$ を $i+1$ 番目に移動させ, $B_{i+1}$ と同じになるようにするためにかかるコストは
$dp[i+1][S \cup \{A_j\}] = dp[i][S] + (i+1 \text{と} A_j が今ある位置の距離) \times Y + \mathrm{abs}(A_j - B_{i+1})$
となる. ここで $dp[0][0] = 0$.
$(i+1 \text{と} A_j が今ある位置の距離)$ について考える. 今 $S$ を整数で表し $k$ 番目(0-index)の bit が立っているとき $A_{k+1} \in S$ とする. 例: $S = 00101 \rightarrow A_{1}, A_{3} \in S$.
$i$ 番目までの文字が決定したとき, $i+1 ~ N$ 番目の文字の位置関係はもとの数列の位置関係と同じであるから(バブルソートが安定なソートであることからもわかる) $A_j \notin S$ の位置と $i+1$ 番目の距離は, $S$ の整数表現を 0 bit 目から見ていき $j-1$ 番目までに含まれる 0 の個数と一致する.
例: $i = 2 \wedge S = 00101$ のとき, $A^\prime = A_1 A_3 A_2 A_4 A_5$ or $A^\prime = A_3 A_1 A_2 A_4 A_5$ となり, $j = 2$ のとき $S$ の $j - 1 = 1$ 番目までに含まれる 0 の個数は 0 個のため $A_2$ の位置と $i+1$ の差は 0, 同様にして $j = 4$ のとき $S$ の $j - 1 = 3$ 番目までに含まれる 0 の個数は 1 個のため $A_4$ の位置と $i+1$ の差は1. … となる.
以上のことを踏まえると下記のようになり, $O(N^2 2^N)$ で解ける.
dp[0][0] = 0;
rep2(i, 1, N + 1) {
rep(S, 1 << N) {
rep(j, N) {
if ((S & (1 << j)) > 0)
continue;
chmin(dp[i][S | (1 << j)], dp[i - 1][S] + get(S, j) * Y + abs(A[j + 1] - B[i]) * X);
}
}
}
上記のコードでは $i$ でループを回しているが, $S$ に立っている bit 数からも求めることができるので以下のようにもかける. このときの計算量は $O(N2^N)$.
vector<ll> dp(1 << N, INF);
dp[0] = 0;
rep(S, 1 << N) {
rep(j, N) {
if ((S & (1 << j)) > 0)
continue;
ll i = __builtin_popcountll(S | (1 << j));
chmin(dp[S | (1 << j)], dp[S] + get(S, j) * Y + abs(A[j + 1] - B[i]) * X);
}
}