ABC 233
Table of Contents
C - Product
$\displaystyle \prod^N_{i=1}L_i \leq 10^5$ より, 考えうるボールの取り出し方を全通り試しても $O(10^5)$ なので全探索する.
$1 \leq a_{i,j} \leq 10^9$ と $N \geq 2$ より, $10^9$ という数が3回以上掛けることがありうるが, 倍精度整数で表現できる整数の範囲はたかだか18桁なので愚直に積を取ると途中でオーバーフローしてしまう. 掛け算をしている途中で $X < \text{(それまでの積)} \times a_{i,j}$ としたいがこのままだと右辺がオーバーフローする可能性があるので, $X / \text{(それまでの積)} < a_{i,j}$ とする.
void dfs(int depth, ll prod) {
if (depth == N) {
if (prod == X) ans++;
return;
}
for (ll x : a[depth]) {
// X < x*prod
if (X / prod < x) continue;
dfs(depth+1, prod*x);
}
}
このオーバーフロー対策を入れないと
3 200376420520689664
1 100000000
1 100000000
1 10000000
という入力のときに 1 と誤った結果が返ってくる.
オーバーフローすることを考えて $X$ の値を慎重に選ばれると間違った答えを返してしまう.
D - Count Interval
$A_i$ の累積和を $\mathrm{cum}[x] = A_0 + \cdots + A_{i-1}$ とする. $r$ を右端とするような連続部分列の要素の和が $K$ となるときの場合の数は $\mathrm{cum}[r+1] - \mathrm{cum}[l] = K$ $(l < r)$ を満たす $l$ の個数と一致する. よって $\mathrm{cum}$ を1番目から順に見ていき, それまでに出た数字の個数をメモしておくことで高速に計算することができる.
E - Σ[k=0..10^100]floor(X/10^k)
$k = 10^{100}$ のとき $\displaystyle 10^{10^{100}}$ となり, また $X$ の上限が $10^{500000}$ であるから, sum の non-zero となる要素の数はたかだか $500000$ 個である.
1桁目から順に値を決めていくことで答えが出せる.
$X = 1225$ のときを例に考える.
1225
122
12
1
題意の sum の要素を桁を揃えて書くと上のようになる. これより最終的な sum の 1の位の数は 1225 の各位の数を足して 10 で割ったあまり. 和の 10 の位の数は 1 の位からの繰り上がりと, 1225 の 10の位から1000の位までの数を足して 10 で割ったあまり … と求めていくことができる.
F - Swap and Sort
swap 操作できる $(a_i, b_i)$ の組をグラフの辺みなし木を構成する. (木が構成できれば連結成分については任意の順番に並び替えることができるので閉路をつくるような辺は無視していい. ) また各ノードは key を持つとする.
最終的にノード $i$ が key として値 $i$ を持つ状態にすることが目標.
昇順に並び替えることができるか否かは node $i$ と node $P_i$ が同じ木に属しているかを調べることで判定が可能. 属していなければどんなに swap しても昇順に並び替えることは不可能であり, 同じ木に属していれば swap 操作を繰り返すことでノード $i$ が key として $i$ を持つことができる. 同じ木に属しているか調べるには Union Find を使うと楽.
深いノードから順にノード $i$ が key $i$ を持つように swap 操作をしていく. 深さ順に確定させる理由は一度決まるとそれ以降 swap 操作をする必要がなくなるため.
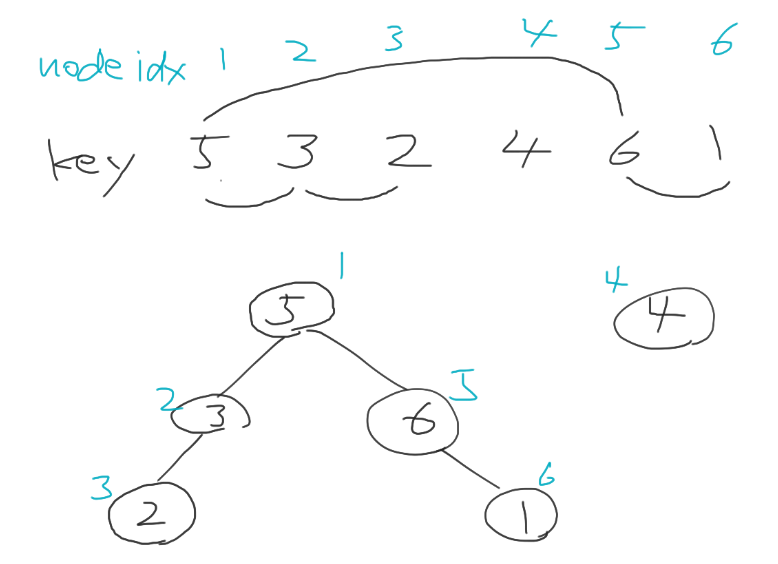
あとは葉から目当ての key までの経路を探し, 経路から操作手順を復元すればよい.
ノードの数が最大でも 1000 なので, 深さは最大でも 999 (root を 0 とした場合). よって root にある key を葉に移動させるために必要な swap 数は最大でも 999. root にある key を葉の親に移動させるのに必要な swap 数は最大でも 998 … となるので 昇順に並べ替えるのに必要な sawp 数は最大でも $999 + 998 + \cdots + 1 = \frac{1000 \times 999}{2} = 499500$ となり愚直に swap しても制約の $5\times 10^5$ 以内に収まる.