ABC 238

Table of Contents

A - Exponential or Quadratic

問題

愚直に $2^n$ を計算すると $n$ が最大で $10^9$ のためオーバーフローする.

$n$ が十分大きいところでは $2^n > n^2$ となるため, そのようなところを探す.

$n = 2, 3, 4$ のときは題意は false であるがそれ以外では true となる.

提出コード

B - Pizza

問題

時計回りか反時計回りかは本質的ではなく, 単に $a_i$ 度のところに切り込みを入れたら, 次は $a_i + a_{i+1}$ 度のところに切り込みを入れていくということを繰り返せば良い. 切り込みを入れた角度を配列に入れ昇順にソートし, 切り込み間の角度を調べ最大のものを出力すれば良い. 番兵として 360 を入れておくと端の処理が楽になる.

void solve() {
    int n;
    cin >> n;
    int now = 0;
    vint angles = {0, 360};
    rep(i, n) {
        int a;
        cin >> a;
        now = (now + a) % 360;
        angles.push_back(now);
    }
    sort(all(angles));
    int ans = 0;
    rep2(i, 1, angles.size()) {
        chmax(ans, angles[i] - angles[i - 1]);
    }
    cout << ans << endl;
}

提出コード

C - digitnum

問題

まずは実験してみる

$\displaystyle \sum_{x = k \text{桁の数}} f(x) = \sum_{i = 1}^{m} \frac{m(m+1)}{2}$ where $m = 9 \times 10^{k-1}$ となる.

$k-1$ 桁の数までは上の式で足していき, $k$ 桁目からの寄与は $\displaystyle \sum_{i = 1}^{N-10^{k-1}+1} i$ を足す.

mint sum(ll x) {
    return mint(x + 1) * x / 2;
}

void solve() {
    ll n;
    cin >> n;

    ll l = 1;
    mint ans = 0;
    while (l <= n) {
        ll r = min(n + 1, 10 * l);
        ll len = r - l;
        ans += sum(len);
        l *= 10;
    }
    cout << ans.val() << endl;
}

提出コード

D - AND and SUM

問題

解説 AC

$s = x + y$, $a = x \text{ AND } y$, $b = x \text{ XOR } y$ とすると $s = 2a + b$ となる.

ビットごとに見ると半加算器の動きになっている. carry の部分が AND で sum の部分が XOR に対応. carry の部分は左に 1 bit シフトするために 2 を掛けている.

問題の題意を満たすためには $b$ が non-zero である必要があるから $s - 2a \geq 0$ であり, かつ XOR と AND の性質から $(s-2a) \text{ AND } a = 0$ となる必要がある.

これらの条件を満たすとき, $x = a, y = s - a$ は題意を満たすため, 上記の条件が必要十分条件となる.

解説放送で桁 DP のやりかたも紹介されていた.

参考

2025/2/23 追記

$x \text{ AND } y = a$ より $x$, $y$ ともに $a$ と同じところに bit が立っている。それ以外の場所は片方は bit が立っているかもしくは両方とも bit が立っていない。 $a$ の bit が立っている場所の集合を $A$, bit が立っていない場所の集合を $B$ とすると $j \in B$ 番目の bit が $x$ で立っているか、$y$ で立っているかは結果に影響しない。そのため $y$ 側で $j \in B$ 番目の bit を立てるかコントロールして $x = a$ としても問題ない。 すると $y = s - x = s - a$ となる。

$x,y$ は非負整数であるから $y \geq 0 \wedge (a \text{ AND } (s-a) = a)$ が成り立つか確認すれば良い。

void solve() {
    ll t;
    cin >> t;

    auto cal = [&](ll a, ll s) {
        ll x = a, y = s - a;
        yesno(y >= 0 && (x & y) == a);
    };

    rep(i, t) {
        ll a, s;
        cin >> a >> s;
        cal(a, s);
    }
}

E - Range Sums

問題

解説 AC

区間をグラフで考える問題

a の index を 0-index で考える.

$b_0 = 0$, $b_r = a_0 + \cdots a_{r-1}$ とすると, 高橋くんは $b_r - b_{l-1}$ の情報を各クエリでくれることになる. 最終的には $a_0 + \cdots + a_{n-1}$ であるが, これは $b_n - b_0$ の情報がわかることと等価である.

各クエリで与えられる情報を node $l-1$ から node $r$ へ辺を張ることと考えるとグラフの問題としてみることができる.

$b_0 = 0$ から出発し, $b_3 - b_0$ の情報から $b_3$ がわかる. $b_3$ と $b_3 - b_2$ の情報から $b_2$ がわかる. $b_2$ と $b_n - b_2$ の情報から $b_n$ がわかる.

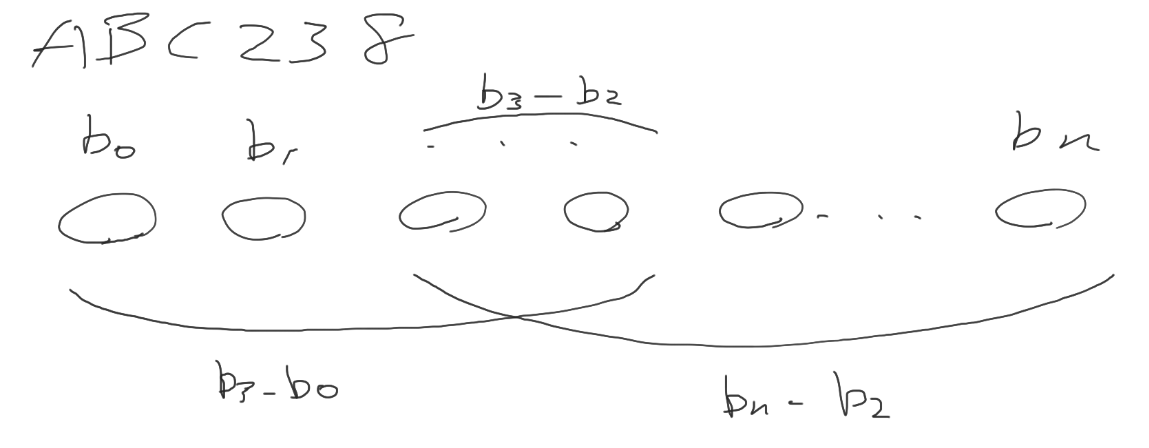
abc238_e

このように $0$ から出発し, $n$ にたどり着くような経路があれば $\sum_i a_i$ を特定することが可能であり, そうでない場合は特定できない. $0$ から $n$ までの経路があるか調べる方法は様々考えられるが, 単に連結性だけがわかればよいので Union Find で調べるのが楽.

提出コード