ABC 240
Table of Contents
A - Edge Checker
$|a-b| = 1$ または $a = 1, b = 10$ のときは Yes, それ以外のときは No
B - Count Distinct Integers
$N$ 個の要素全部 set に突っ込んで最後に size を出力
C - Jumping Takahashi
$dp[i][x]$ を $i$ 回目のジャンプで座標 $x$ に行けるかとし 初期値 $dp[0][0] = true$ とする.
$dp[i-1][x] = true$ ならば $dp[i][x+a] = dp[i][x+b] = true$ に更新する.
D - Strange Balls
筒の中に入っているボールの数を同じ数字が書かれたボールに関しては圧縮してもつ.
筒の中に [2, 3, 3, 2, 4, 4, 4, 5] と入っていたら
[{2, 1}, {3, 2}, {2, 1}, {4, 3}, {5, 1}] という風に {数字, 個数} として保持する.
新たなボールを加えるときは最後尾のペアを見て数字が同じだったら個数を増やす, 違ったらペアを増やすとしていく. 個数を増やした結果数字と個数が一緒になったらそのペアは配列から削除する.
E - Ranges on Tree
入れ子集合モデルを知っていると比較的簡単に実装方針が立ったのではないかと思う.
ref 第5回 SQLで木構造を扱う~入れ子集合モデル (1)入れ子集合モデルとは何か
まず葉の数字は $L_i = R_i$ とするのが最適. そうでなければ無駄に $\max \{L_i, R_i\}$ の値が大きくなってしまう.
また
- $S_i \subseteq S_j \Rightarrow [L_i, R_i] \subseteq [L_j, R_j]$
- $S_i \cap S_j = \empty \Rightarrow [L_i, R_i] \cap [L_j, R_j] = \empty$
より, 全ての葉は違う数字を振るのが最適である. 葉以外のノードでは $L_i = \min{\text{全ての子ノードの } L}$, $R_i = \max{\text{全ての子ノードの } R}$ というのを 葉の方から決めていけば良い.
ここで, 葉に振る数字は DFS での訪れた順に数字を振らなければならない. 葉への数字の振り方がいい加減だと WA になる.
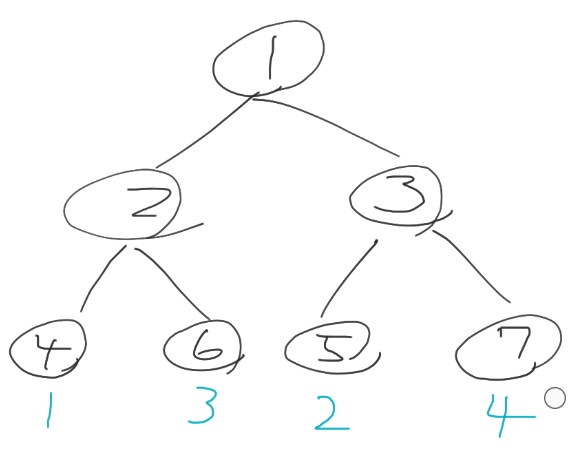
例えば下図のようなときに, 葉ノード 4, 5, 6, 7 に数字を1から連番で振ると図の
ようになるが, これでは $S_2 \cap S_3 = \empty$ なのに $[1, 3] \cap [2, 4] \neq \empty$ になってしまう.
そのため, 葉への数字の割り振りは DFS で訪れた順でないといけない.
int n;
vvint graph;
// P: L, R
vector<P> ans;
int num = 1;
void dfs(int x, int p) {
// leaf
if (x != 0 && graph[x].size() == 1) {
ans[x] = {num, num};
num++;
return;
}
ll mn = INF, mx = -INF;
for (int nx : graph[x]) {
if (nx == p)
continue;
dfs(nx, x);
chmin(mn, ans[nx].first);
chmax(mx, ans[nx].second);
}
ans[x] = {mn, mx};
}
void solve() {
cin >> n;
graph.resize(n);
ans.resize(n, {INF, -INF});
rep(i, n - 1) {
int u, v;
cin >> u >> v;
u--, v--;
graph[u].push_back(v);
graph[v].push_back(u);
}
dfs(0, -1);
for (auto [l, r] : ans) {
cout << l << ' ' << r << endl;
}
}