ABC 243

Table of Contents

##
[問題]()
[提出コード]()

A - Shampoo

問題

単純にシミュレーションをするか, $V <= A+B+C$ のときは3人が1順するごとに $A+B+C$ 減るので $V$ を V % (A + B + C) スタートにしても問題ない. この状況で誰が使うときに不足するかを調べればよい.

void solve() {
    int v, a, b, c;
    cin >> v >> a >> b >> c;

    v %= a + b + c;
    if (v - a < 0) {
        cout << "F" << endl;
        return;
    }
    v -= a;
    if (v - b < 0) {
        cout << "M" << endl;
        return;
    }
    cout << "T" << endl;
}

提出コード

B - Hit and Blow

問題

愚直に2重ループを回して条件に合う数を調べれば良い. $A$, $B$ ともにすべての要素が異なるので片方の数列の要素の index を map に保存しておき もう片方の数列の要素でループを回し, map に保存した index と一致するか否かを判定する方法だと $O(N)$ で解ける.

提出コード

C - Collision 2

問題

同じ $y$ 座標上に2人以上いなければ衝突は起こらないので, 2人以上いる $y$ 座標について考える. このとき, 右を向いている人の $x$ 座標の最小値が, 左を向いている $x$ 座標の最大値よりも小さければ 時間が経つと衝突する.

void solve() {
    int n;
    cin >> n;

    vint x(n), y(n);
    rep(i, n) cin >> x[i] >> y[i];

    string dir;
    cin >> dir;

    map<int, int> left, right;
    rep(i, n) {
        if (dir[i] == 'L') {
            if (left.count(y[i]))
                chmax(left[y[i]], x[i]);
            else
                left[y[i]] = x[i];
        } else {
            if (right.count(y[i]))
                chmin(right[y[i]], x[i]);
            else
                right[y[i]] = x[i];
        }
    }

    for (auto it = right.begin(); it != right.end(); it++) {
        if (it->second < left[it->first]) {
            cout << "Yes" << endl;
            return;
        }
    }

    cout << "No" << endl;
}

上記のコードにおいて if (left.count(y[i])) のように $y$ 座標がすでにあるかのチェックを入れないと left[y[i]] が 0 を返してしまい存在しない $x$ 座標の値が入ってしまうことがあるので注意!

提出コード

D - Moves on Binary Tree

問題

LU または RU と移動するとき, もとの場所に戻るのでこれらの移動は無視して良い. 与えられた文字列に対して LU, RU となる部分を削除する操作を繰り返して得られた文字列を $S'$ とすると, 先頭に U が並び, それ以降は L or R のいずれかの文字が連続する文字列となる. これ以上省略した操作はなく, 答えが $10^{18}$ 以下になることが保証されているので あとは $X$ スタートで $S'$ の通りの操作を行うと答えを求めることができる.

$S'$ の構築方法としては stack を使い以下のような手順で構築すればよい

最終的に stack に残った文字を stack の底にあるものから順に並べると $S'$ を構築できる. 最終的に欲しいのは追加した順なので実際は stack でなく vector や deque を使って実装するほうが楽.

void solve() {
    ll n, x;
    cin >> n >> x;
    string s;
    cin >> s;

    string mv = "";
    rep(i, n) {
        if (mv.size() != 0 && mv.back() != 'U' && s[i] == 'U')
            mv.pop_back();
        else
            mv.push_back(s[i]);
    }

    ll ans = x;
    for (char c : mv) {
        if (c == 'U')
            ans /= 2;
        if (c == 'L')
            ans *= 2;
        if (c == 'R')
            ans = ans * 2 + 1;
    }
    cout << ans << endl;
}

$X$ を2進数を表した文字列を作り

E - Edge Deletion

問題

解説 AC

最小全域木で良さそうに見えるが以下のパターンのように最小全域木では2点間の最短経路は保証されない.

e.png

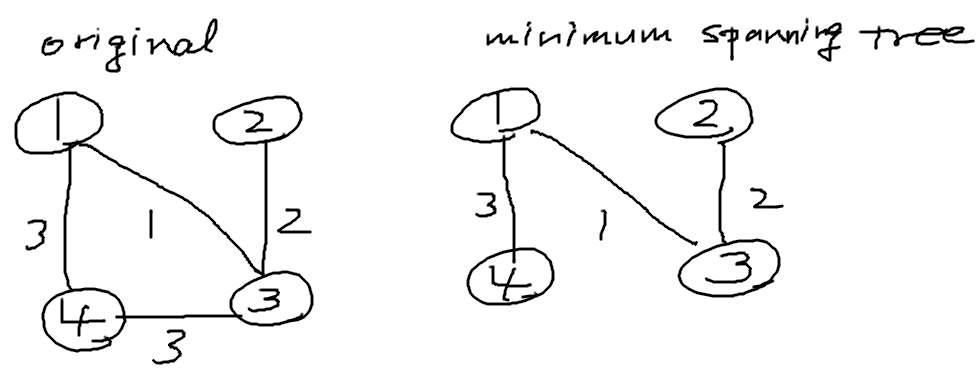
頂点 $i$, $j$ 間の最短距離を $d_{i,j}$ とする. まずワーシャルフロイドで任意の2点間の距離を求める. このとき, 後々のために $d_{i,i} = \infty$ としておく.

辺 $i$ を削除しても任意の2点間の距離が変わらないのは $A_ii$, $B_i$ の path のコストが $C_i$ 以下となるような経路が辺 $i$ 以外に存在するときである.

よって 辺 $i$ を削除してよいかは $d_{A_i, k} + d_{k, B_i} \leq C_i$ となる $k$ が存在するか否かを判定すればよい.

提出コード