ABC 353
Table of Contents
https://atcoder.jp/contests/abc353
A. Buildings
https://atcoder.jp/contests/abc353/tasks/abc353_a
B. AtCoder Amusement Park
https://atcoder.jp/contests/abc353/tasks/abc353_b
C. Sigma Problem
https://atcoder.jp/contests/abc353/tasks/abc353_c
D. Another Sigma Problem
https://atcoder.jp/contests/abc353/tasks/abc353_d
E. Yet Another Sigma Problem
https://atcoder.jp/contests/abc353/tasks/abc353_e
$0 \sim i-1$ 文字目が同じで $i$ 文字目も同じであるような文字列の数が $N_i$ 個あったとすると、$i$ 文字目の寄与は $\binom{N_i}{2}$ である。 Trie を使って、これらの個数を数える。各ノードの共有している文字列の数は入力例2では以下のようになる。
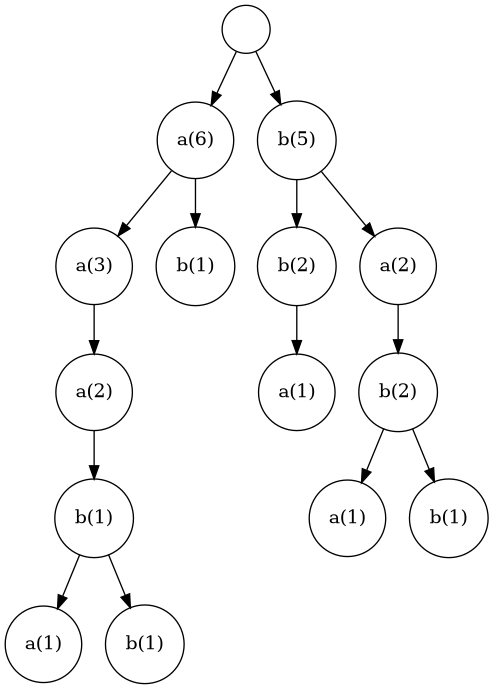
\begin{align*} &\binom{6}{2} + \binom{3}{2} + \binom{2}{2} + \binom{5}{2} + \binom{2}{2} + \binom{2}{2} + \binom{2}{2} \\ &= 15 + 3 + 1 + 10 + 1 + 1 + 1 \\ &= 32 \end{align*}
類題: ABC 403 E
struct Trie {
vector<map<char, int>> to;
vll cnt;
Trie()
: to(1), cnt(1) {};
int add(string s) {
int v = 0;
for (char c : s) {
if (to[v].count(c) == 0) {
int u = to.size();
to.push_back(map<char, int>());
to[v][c] = u;
cnt.push_back(0);
}
v = to[v][c];
cnt[v]++;
}
return v;
}
};
void solve() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int N;
cin >> N;
vector<string> S(N);
rep(i, N) cin >> S[i];
Trie trie;
for (string s : S)
trie.add(s);
ll ans = 0;
for (ll x : trie.cnt) {
ans += x * (x - 1) / 2;
}
cout << ans << endl;
}
F. Tile Distance
https://atcoder.jp/contests/abc353/tasks/abc353_f