ABC 389

Table of Contents

C

https://atcoder.jp/contests/abc389/tasks/abc389_c

deque にヘビの頭の座標と長さを入れる。 タイプ2 で全体の要素の座標を更新すると要素数分更新する必要があるので非効率。出ていったヘビの長さを記録しておき、あとからその値を引く

void solve() {
    ll Q;
    cin >> Q;

    ll sub = 0;

    // head pos, length
    deque<pair<ll, ll>> que;
    rep(i, Q) {
        ll x;
        cin >> x;
        if (x == 1) {
            ll l;
            cin >> l;
            if (que.size()) {
                auto [prevpos, prevlen] = que.back();
                que.push_back({prevpos + prevlen, l});
            } else {
                que.push_back({0, l});
            }
        } else if (x == 2) {
            auto [pos, len] = que.front();
            que.pop_front();
            sub = pos + len;
            if (que.empty())
                sub = 0;
        } else {  // x==3
            ll k;
            cin >> k;
            k--;
            cout << que[k].first - sub << endl;
        }
    }
}

D

https://atcoder.jp/contests/abc389/tasks/abc389_d

正方形の頂点の位置が整数でなく扱いづらいので整数の問題に変換する。

頂点 $(x,y)$ は整数 $X, Y$ を用いて

\begin{align} x &= X + \frac{1}{2} = \frac{2X+1}{2} \\ y &= Y + \frac{1}{2} = \frac{2Y+1}{2} \end{align}

とかける。

よって \begin{align} &x^2 + y^2 \leq R^2 \\ &\left( \frac{2X+1}{2} \right)^2 + \left( \frac{2Y+1}{2} \right)^2 \leq R^2 \\ & (2X+1)^2 + (2Y+1)^2 \leq 4R^2 \end{align} より、$(2X+1)^2 + (2Y+1)^2 \leq 4R^2$ を満たす整数 $(X,Y)$ の問題として考える。

例えば、$(X,Y) = (0,0)$ はもとの座標の $(1/2, 1/2)$ なので原点中心の正方形の右上の座標に対応する。

上下左対称なので第1象限にある正方形の右上の座標に着目する。

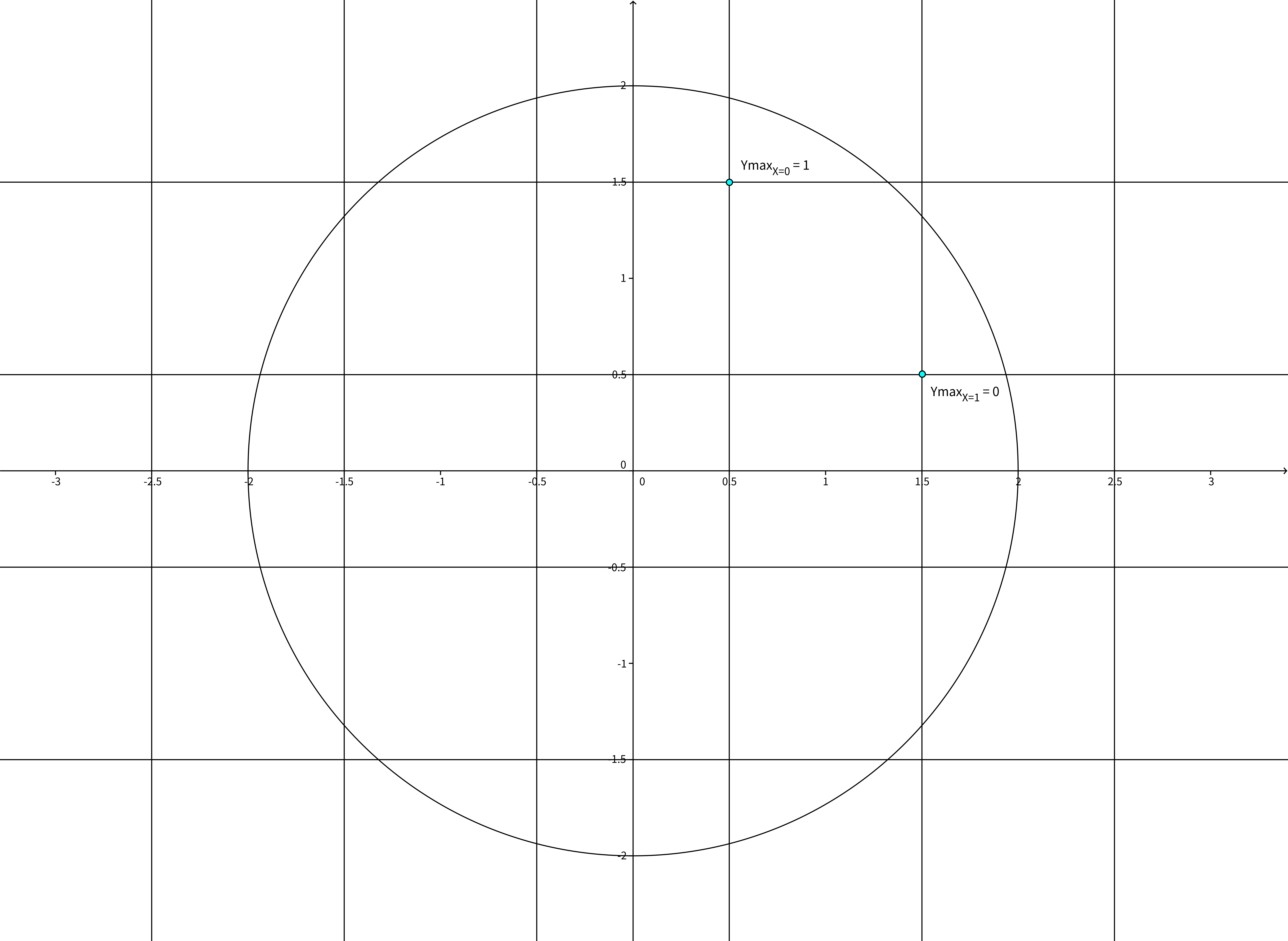
$X$ を固定したときの条件を満たす最大の非負整数 $Y$ の値を $Y_{\mathrm{max}}$ とすると、$Y_{\mathrm{max}}$ がその $X$ のときの一番上にある正方形の右上の座標に対応する。上下対称なので $2 Y_{\mathrm{max}} + 1$ の正方形がある($Y=0$ で $+1$ している)。$X\neq 0$ のときは左側にも同じ数だけあるのでさらに2倍する。 $X=0, Y=R$ から始めて条件を満たしたら $X$ を increment, 満たさなかったら満たすまで $Y$ を decrement すれば答えが出せる。

abc389_d.png

void solve() {
    ll R;
    cin >> R;

    ll ans = 0;
    ll y = R;
    ll x = 0;
    while (y >= 0 && x <= R) {
        ll dx = 2 * x + 1;
        ll dy = 2 * y + 1;
        if (dx * dx + dy * dy <= 4 * R * R) {
            if (x != 0)
                ans += (2 * y + 1) * 2;
            else
                ans = (2 * y + 1);
            x++;
        } else {
            y--;
        }
    }
    cout << ans << endl;
}

E

解説 AC

$i$ 番目の商品を $k$ 個買ったときと $k+1$ 個買ったときの差額は

$$ (k+1)^2 P_i - k^2 P_i = ((k+1)^2 - k) P_i = (2k+1)P_i $$

であるから、$i$ 番目の商品を $k$ 個買っているとき更にもう一つ買う場合は $(2k+1)P_i$ 払う必要があると言いかえることができる。また $k$ 個目の値段は $(2k-1)P_i$ 円とも言える。

これらの値段を priority queue に入れて貪欲に安い方から順に買っていけば正しい答えが出せるが制約からこの方式だと TLE する。

安い順に買うのが最適だから買った商品の値段は最後に買った商品以下に必ずなる。この最後に買った商品の値段で二分探索をすることで高速に解を求めることができる。

最後に買った商品の値段「以下」基準だと同じ値段が合った時の処理が面倒になるので最後に買った商品の値段未満の商品をすべて買ったときのことを考える。 $x$ 円未満の商品をすべて買ったときに合計が $M$ 円以下となる最大の $x$ の値を求めて、最後に余ったお金で $x$ 円のものを買うことにする。

ll N, M;
vll P;
ll tot, num;

// x 円未満の商品をすべて買うことができるか
bool judge(ll x) {
    tot = num = 0;
    rep(i, N) {
        // x 円未満となる最大の k を求める
        // (2k-1)Pi < x
        // -> (2k-1)Pi <= x-1 (すべてが整数だからこれが言える)
        ll k = ((x - 1) / P[i] + 1) / 2;
        if (k == 0)
            continue;

        // tot 計算の overflow 対策
        if (M / k / k / P[i] == 0) {
            // M を超えるので ng
            return false;
        }
        tot += k * k * P[i];
        num += k;
        if (tot > M)
            return false;
    }
    return true;
}

void solve() {
    cin >> N >> M;
    P = vll(N);
    rep(i, N) cin >> P[i];

    // judge(x) が true を返す最大の x を探索
    ll ac = 0, wa = M + 1;
    while (abs(ac - wa) > 1) {
        ll x = (ac + wa) / 2;
        if (judge(x))
            ac = x;
        else
            wa = x;
    }

    // 二部探索終了時に ac 側で終わったのか wa 側で終わったかによって
    // tot, num の値が変わるので改めて ac の値で計算
    judge(ac);
    num += (M - tot) / ac;
    cout << num << endl;
}

最後に ac 円のものを買っているが、商品の中に ac 円のものが (M-tot)/ac 個あるとしてよいのか何故か？

ac は judge(x) を満たす最大の $x$ であるから、judge(x) = true, judge(x+1) = false である。 これはどういうことかというと ac 円未満のものはすべて買えるが、ac+1 円未満をすべては買えないということである。 ac 未満では買えないが ac+1 未満で新規で買えるようになるのは ac 円の商品である。よって ac 円の商品は必ず存在する。また ac 円のものをすべて買うと $M$ を超えることから M-tot で買えるだけの ac 円の商品の在庫が必ず存在する。