ARC 122
Table of Contents
A - Many Formulae
$dp[i][x]$: $i$ 番目までの数字を使う, かつ, $A_i$ を $x~(x = + \text{ or } -)$ とするような式の合計とする.
具体的に書いてみるとわかりやすいが, 遷移は以下のようになる.
\begin{align} dp[i][+] &= (dp[i-1][+] + dp[i-1][-]) + (i-1 \text{ までを使ったときの式の場合の数}) \times A_i \ dp[i][-] &= dp[i-1][+] - (A_{i-1} \text{を足したときの式の場合の数}) \times A_i \end{align}
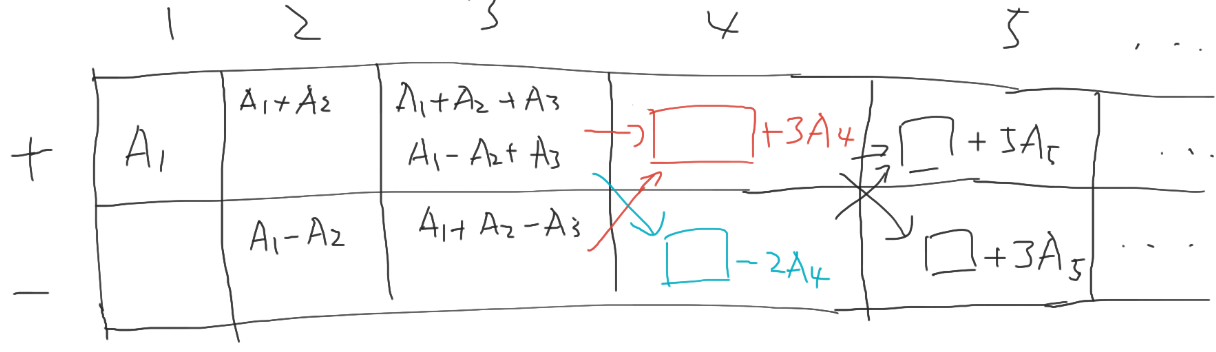
掛け合わせる数はフィボナッチ数列になっている. $DP$ テーブル一つだけで処理するのは面倒(pair を使って合計と個数を記録していればできる)なので掛ける数は別にテーブルに保持しておくと楽
void solve() {
int n;
cin >> n;
vector<ll> a(n + 1);
rep(i, n) cin >> a[i + 1];
vector<vector<mint>> dp(n + 1, vector<mint>(2, 0)), mul(n + 1, vector<mint>(2, 0));
dp[1][0] = a[1];
mul[1][0] = 1;
rep2(i, 2, n + 1) {
mul[i][0] = mul[i - 1][0] + mul[i - 1][1];
mul[i][1] = mul[i - 1][0];
dp[i][0] = dp[i - 1][0] + dp[i - 1][1] + mul[i][0] * a[i];
dp[i][1] = dp[i - 1][0] - mul[i][1] * a[i];
}
cout << (dp[n][0] + dp[n][1]).val() << endl;
}