ARC 132
Table of Contents
A - Permutation Grid
1-index で考え, grid の $A$ と呼ぶことにする.
公式解説の通り, $R$, $C$ の並び方がともに $1, 2, \cdots, n$ である場合は, 上から $r$ 行目, $c$ 行目のマスが $r+c \geq n + 1$ である場合に黒で, それ以外では白となる.
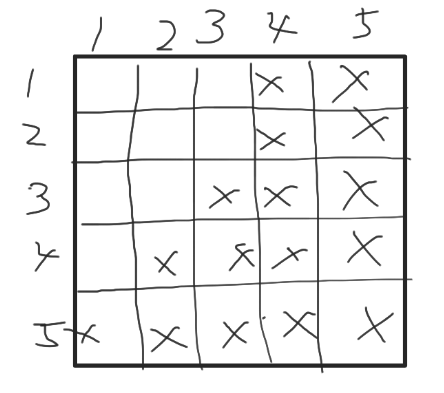
ここで行 $i$, $j$ を入れ替えたとき $C_1, \cdots, C_n$ の結果に影響を与えない. 同様に列 $i$, $j$ を入れ替えたとき $R_1, \cdots, R_n$ の結果に影響を与えない.
$R_i$, $C_i$ が昇順になるように行・列の入れ替えを行ってできる grid を $A^\prime$ としたとき $A$ の $(r, c)$ 成分が $A^\prime$ のどの成分に対応するか調べることでマスが黒か白か判定できる.
$R$, $C$ は $1, \cdots, n$ の順列だから, ソートによって $r$ 行目は $R_r$ 行目に, $c$ 列目は $C_c$ 列目に移動する. よって $R_r + C_c \geq n+1$ のとき黒, それ以外のときは白となる.
一般化して考えてみる
この説明は間違っている. 例 $R = \{0, 1, 1, 1, 1\}$, $C =\{0, 1, 1, 1, 1\}$ のとき崩壊
1-index で考える.
$R$, $C$ が $1, \cdots, n$ の順列でない場合を考える.
$R$, $C$ が降順に並び替えたものをそれぞれ $R^\prime$, $C^\prime$ とし, 行・列をこれにならうように並び替える. 並び替えによって元々 $r$ 行目が $r^\prime$ 行目に, $c$ 列目が $c^\prime$ 列目に移動したとすると, $r^\prime \leq C^\prime[c^\prime] \wedge c^\prime \leq R^\prime[r^\prime]$ のとき黒で, それ以外のときは白になる.
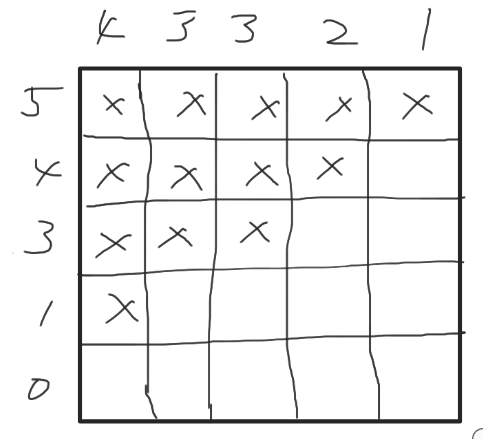 $R = \{5, 4, 3, 1, 0 \}, C = \{4, 3, 3, 2, 1\}$ のときの例
$R = \{5, 4, 3, 1, 0 \}, C = \{4, 3, 3, 2, 1\}$ のときの例
B - Shift and Reverse
- 操作1: 全体をひっくりかえす. つまり, $p_1, \cdots, p_n$ を $p_n, \cdots, p_1$ に並び替える.
- 操作2: 先頭の項を末尾に移動させる. つまり $p_1, \cdots, p_n$ を $p_2, \cdots, p_n, p_1$ に並び替える.
とする.
$1 \sim n$ に操作1, 操作2 を複数回作用させてできる数列は次の2パターンある.
- (i) 1の右隣りに2がある. (1が末尾のときは2が先頭にある)
- (ii) 1の左隣りに2がある. (1が先頭のときは2は末尾にある)
※ 順列 $1, \cdots, n$ に 操作1, 操作2 を作用させるということは $1, \cdots, n$ を円に沿って並べて, 左に1つずらしたり(操作2), 左右反転(操作2)させているだけなので上の (i), (ii) の2通りのパターンしかできない.
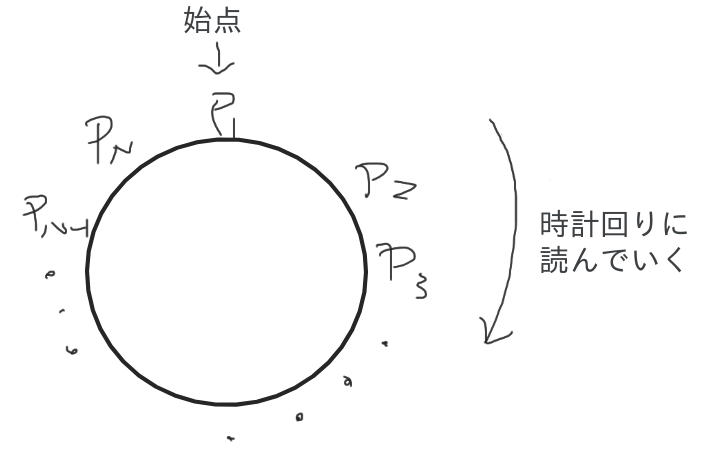
1のある index を $k$ とする. (0-index)
(i) のとき
ex. 5671234
昇順に並べる方法は次の2通りある
- 1より左にある要素を末尾にすべて移動させるか
- 操作2 を $k$ 回する
- 操作1をして降順になるまで操作2を行い, 最後にまた操作1をする
- 4321765 -> 7654321 -> 1234567
- 操作1を2回
- 操作2を $n-k$ 回
- 合計 $n-k+2$ 回
2通りのうち操作回数が少ないほうが答え. $\min(k, n-k+2)$
(ii) のとき
ex. 4321765
昇順に並べる方法は次の2通り
- 降順になるまで操作2をしたあとに操作1をする
- 4321765 -> 7654321 -> 1234567
- 降順になるまで操作2を行う回数. $k+1$ 回
- 操作1を行う. 1回
- 合計 $k+2$ 回
- 操作1をしたあとに昇順になるまで操作2を繰り返す
- 5671234 -> 1234567
- 操作1を行う. 1回
- 昇順になるまで操作2を行う. $n - (k+1)$ 回
- 合計 $n-k$ 回
2通りのうち操作回数が少ないほうが答え. $\min(k+2, n-k)$