ARC 133
Table of Contents
A - Erase by Value
$A_i > A_{i+1}$ となる最初の $A_i$ を消したときが辞書順最小となる.
$A_i < A_{i+1}$ となる $A_i$ を消した場合, 辞書順であとにくる数列に変化してしまうので数列が広義単調増加しているうちはその文字は消すべきではない.
B - Dividing Subsequence
LCS の亜種. 「$b_i$ は $a_i$ の倍数」という条件を $a_i = b_i$ に変えると LCS と同じになる. ただし, LCS を使うと計算量が $O(N^2)$ になってしまうので, そのままでは適用することができない.
$Q_j$ が $P_i$ の倍数となるような index のペア $(i,j)$ に関して, 第1要素で昇順, 第2要素で降順に並べたものに対して, 第2要素の LIS の長さを求めると問題の答えになる.
入力例を使って実際に考えてみる.
3 1 4 2
4 2 1 3
このとき, ペアを辺と捉えると下図のようになる.
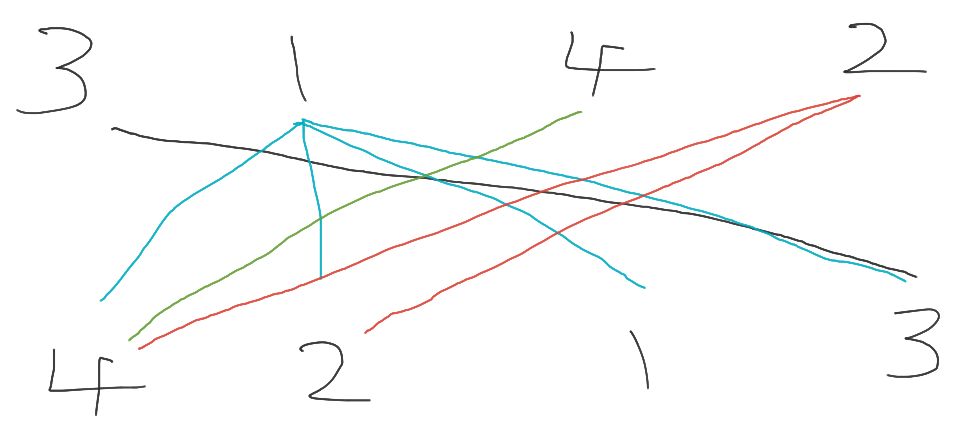
ここで, 辺を交差しないようにできるだけ多く選択したい. 第1要素を横軸, 第2要素を縦軸に辺をプロットすると下図のようになる.
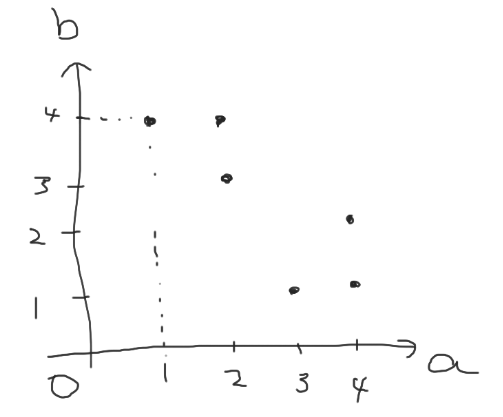
これより, 2辺 $(a_i, b_i)$, $(a_j, b_j)$ が交差しないための条件は $a_i < a_j \wedge b_i < b_j$ が成り立つことである. この条件を満たすように辺を選んだときの, 選べる辺の最大値は先に述べたように第2要素の LIS の長さとなる.
書いたことを素朴に実装するとこんな感じ.
void solve() {
int n;
cin >> n;
vint p(n + 1), q(n + 1);
rep(i, n) cin >> p[i + 1];
rep(i, n) cin >> q[i + 1];
vint pid(n + 1), qid(n + 1);
rep(i, n) {
pid[p[i + 1]] = i + 1;
qid[q[i + 1]] = i + 1;
}
// q_j % p_i == 0 となる (i,j) のペアを全列挙
vector<Pair> cand;
rep2(i, 1, n + 1) {
for (int j = i; j <= n; j += i) {
cand.push_back({pid[i], qid[j]});
}
}
// ペアの配列を第1要素に関して昇順, 第2要素に関して降順で sort する
sort(all(cand));
// 2つのペア (a_i, b_i), (a_j, b_j) が交差しないためには a_i < a_j & b_i < b_j が成り立つ必要がある.
// a の方に関してはすでにソートされているので, b の方に関して LIS を計算することで答えが出る
vint lis(n, INF);
for (auto p : cand) {
*lower_bound(all(lis), p.y) = p.y;
}
cout << lower_bound(all(lis), INF) - lis.begin() << endl;
}
上でやっていることは結局 $P_1$ の倍数となるような $Q_i$ の index を降順に並べて LIS テーブルを更新し, $P_2$ の倍数となるような $Q_i$ の index を降順に並べて LIS テーブルを更新し・・・ とやっているだけなので, $P$ 側の index は実はいらない. それを省略すると以下のようになる.
void solve() {
int n;
cin >> n;
vint p(n + 1), q(n + 1);
rep(i, n) cin >> p[i + 1];
rep(i, n) cin >> q[i + 1];
vint qid(n + 1);
rep(i, n) {
qid[q[i + 1]] = i + 1;
}
vint lis(n, INF);
rep2(i, 1, n + 1) {
vint cand;
for (int j = p[i]; j <= n; j += p[i]) {
cand.push_back(qid[j]);
}
sort(rall(cand));
for (int x : cand) {
*lower_bound(all(lis), x) = x;
}
}
cout << lower_bound(all(lis), INF) - lis.begin() << endl;
}