ARC 135
Table of Contents
A - Floor, Ceil - Decomposition
数字 $x$ をそのままにするか, $\lfloor \frac{x}{2} \rfloor$, $\lceil \frac{x}{2} \rceil$ に書き換えるかは $x < \lfloor \frac{x}{2} \rfloor \times \lceil \frac{x}{2} \rceil$ となれば書き換えたほうが全体の積が大きくなり, その他の場合は $x$ のままにするのがよい.
おおよそ $\displaystyle \left\lfloor \frac{x}{2} \right\rfloor \times \left\lceil \frac{x}{2} \right\rceil \approx \frac{x^2}{4}$ となることを考え, $y = x$ と $y = \frac{x^2}{4}$ のグラフを描くと $0 \leq x \leq 4$ の区間では $y = x$ が, $x > 4$ の区間では $y = x^2 / 4$ のほうが大きいことがわかる.
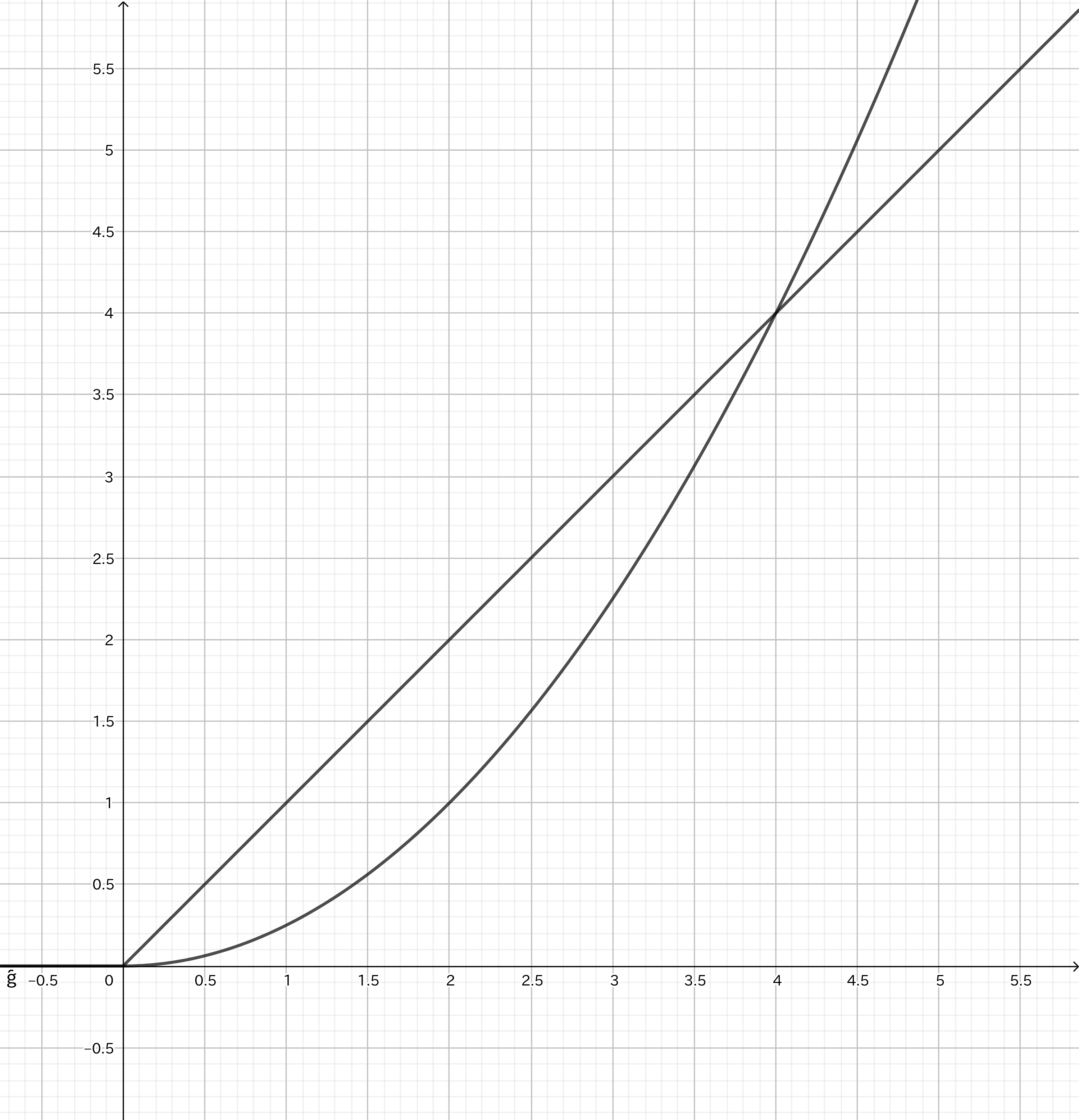
$g(x) = \max(x, \left\lfloor \frac{x}{2} \right\rfloor \times \left\lceil \frac{x}{2} \right\rceil)$ とすると
- $g(1) = \max(1, 0 \times 1) = 1$
- $g(2) = \max(2, 1 \times 1) = 2$
- $g(3) = \max(3, 1 \times 2) = 3$
- $g(4) = \max(4, 2 \times 2) = 4$
- $g(5) = \max(5, 2 \times 3) = 6$
- $\vdots$
となり, $1 \leq x \leq 4$ の区間では $x$ そのまま, $x > 4$ の区間では floor, ceil に分解して積をとったほうが良いことがわかる. ($x = 4$ のときはそのままでも分解してもどちらでも一緒だけれども)
答えは
\begin{align} f(x) = \left\{ \begin{aligned} &x ~~ \text{ if } 1 \leq x \leq 4 \\ &\left\lfloor \frac{x}{2} \right\rfloor \times \left\lceil \frac{x}{2} \right\rceil ~~ \text{ otherwise} \end{aligned} \right. \end{align}
として, $f(X)$ を計算すれば良い.
メモ化を使えば高速に答えを求めることができる.
B - Sum of Three Terms
$S_i = A_i + A_{i+1} + A_{i+2}$ より $A_{i+3} = A_i - (S_i - S_{i+1})$ となる. 具体的に書くと
$A_4 = A_1 - (S_1 - S_2)$
$A_7 = A_4 - (S_4 - S_5) = A_1 - (S_1 - S_2) - (S_4 - S_5)$
$\vdots$
$A_5 = A_2 - (S_2 - S_3)$
$A_8 = A_5 - (S_5 - S_6) = A_2 - (S_2 - S_3) - (S_5 - S_6)$
$\vdots$
$A_3 = S_1 - A_1 - A_2$
$A_6 = S_4 - A_4 - A_5 = S_4 - (A_1 - (S_1 - S_2)) - (A_2 - (S_2 - S_3)) = S_4 + (S_1 - S_2) + (S_2 - S_3) - A_1 - A_2$
$\vdots$.
これより $A_1 = a$, $A_2 = b$ とすると
\begin{align} \left\{ \begin{aligned} A_i &= a + f_i({S_i}) ~~ (i = 1, 4, 7, \cdots) \\ A_i &= b + g_i({S_i}) ~~ (i = 2, 5, 8, \cdots) \\ A_i &= h_i({S_i}) - a - b ~~ (i = 3, 6, 9, \cdots) \end{aligned} \right. \end{align}
と書くことができる.
問題の制約より $A_i \geq 0$ だから $\forall i, a \geq -f_i(\{S_i\}),~ b \geq - g_i(\{S_i\}),~ h_i(\{S_i\}) \leq a + b$ を満たす必要がある.
$c_1 = \max_i \left\\{ -f_i(\{S_i\}) \right\\}$, $c_1 = \max_i \left\\{ -g_i(\{S_i\}) \right\\}$, $c_3 = \max_i \left\\{ h_i(\{S_i\}) \right\\}$
とすると解が存在するためには $c_3 \leq c_1 + c_2$ である必要がある. これを満たすとき $a = c_1, b = c_2$ とすると題意を満たす数列を構築できる.
$c_1, c_2, c_3$ は $a = b = 0$ として $A_{i+2} = S_i - A_i - A_{i+1}$ を計算すれば $f_i, g_i, h_i$ の値が求まるのでそこから計算すればよい.
C - XOR to All
操作は 0 or 1 回しかする必要がない. 2回以上操作してできる数列は1回の操作によってもできる.
まずこれを示す
数列 $A$ から $A_k$ を選んで操作してできた数列を $B$ とすると $B_i = A_i \oplus A_k$ である.
同様にして数列 $B$ から $B_l$ を選んですさしてできた数列を $C$ とすると $C_i = B_i \oplus B_l$ である. ここで $C_i = B_i \oplus B_l = (A_i \oplus A_k) \oplus (A_l \oplus A_k) = A_i \oplus A_l$ となるから, 数列 $C$ は数列 $A$ に $A_l$ を XOR したものと一緒である.
これより2回の操作は必要ないことがわかった.
あとは $A$ のどの要素を選んだときに和が最大になるかを全探索すれば良い. 愚直に調べていくと $O(N^2)$ のオーダーになるので TLE になってしまう. そこで $A$ の全ての数に対して $k$ bit 目が立っている要素の数を記録する. これを使うと $A_k$ と XOR とった数列の和は
$\displaystyle \sum_{i \in A_k \text{ の bit が立っている桁}} (N - r_i) \times 2^i + \sum_{i \in A_k \text{ の bit が折れている桁}} r_i \times 2^i$
と書ける. ここで $r_k$ は $k$ bit 目が立っている要素の数.
$A_i < 2^{30}$ より計算量は $O(30 N)$ となる.